题目内容
已知函数 (a>1),求证:
(a>1),求证:(1)函数f(x)在(-1,+∞)上为增函数;
(2)方程f(x)=0没有负数根.
【答案】分析:(1)证明函数的单调性,一个重要的基本的方法就是根据函数单调性的定义;
(2)对于否定性命题的证明,可用反证法,先假设方程f(x)=0有负数根,经过层层推理,最后推出一个矛盾的结论.
解答:证明:(1)设-1<x1<x2,
则
= ,
,
∵-1<x1<x2,∴x1+1>0,x2+1>0,x1-x2<0,
∴ ;
;
∵-1<x1<x2,且a>1,∴ ,∴
,∴ ,
,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在(-1,+∞)上为增函数;
(2)假设x是方程f(x)=0的负数根,且x≠-1,则 ,
,
即 ,①
,①
当-1<x<0时,0<x+1<1,∴ ,
,
∴ ,而由a>1知
,而由a>1知 .∴①式不成立;
.∴①式不成立;
当x<-1时,x+1<0,∴ ,∴
,∴ ,而
,而 .
.
∴①式不成立.综上所述,方程f(x)=0没有负数根.
点评:(1)函数的单调性就是随着x的变大,y在变大就是增函数,y变小就是减函数,具有这样的性质就说函数具有单调性,符号表示:就是定义域内的任意取x1,x2,且x1<x2,比较f(x1),f(x2)的大小 (当f(x1)<f(x2)则是增函数,当f(x1)>f(x2)则是减函数);
(2)方程的根,就是指使方程成立的未知数的值.对于结论是否定形式的命题,往往反证法证明.
(2)对于否定性命题的证明,可用反证法,先假设方程f(x)=0有负数根,经过层层推理,最后推出一个矛盾的结论.
解答:证明:(1)设-1<x1<x2,
则

=
 ,
,∵-1<x1<x2,∴x1+1>0,x2+1>0,x1-x2<0,
∴
 ;
;∵-1<x1<x2,且a>1,∴
 ,∴
,∴ ,
,∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴函数f(x)在(-1,+∞)上为增函数;
(2)假设x是方程f(x)=0的负数根,且x≠-1,则
 ,
,即
 ,①
,①当-1<x<0时,0<x+1<1,∴
 ,
,∴
 ,而由a>1知
,而由a>1知 .∴①式不成立;
.∴①式不成立;当x<-1时,x+1<0,∴
 ,∴
,∴ ,而
,而 .
.∴①式不成立.综上所述,方程f(x)=0没有负数根.
点评:(1)函数的单调性就是随着x的变大,y在变大就是增函数,y变小就是减函数,具有这样的性质就说函数具有单调性,符号表示:就是定义域内的任意取x1,x2,且x1<x2,比较f(x1),f(x2)的大小 (当f(x1)<f(x2)则是增函数,当f(x1)>f(x2)则是减函数);
(2)方程的根,就是指使方程成立的未知数的值.对于结论是否定形式的命题,往往反证法证明.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
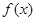 =
=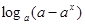 (a>1) .
(a>1) .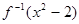 >
>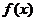 =
=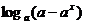 (a>1) .
(a>1) .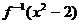 >
>