题目内容
将和式的极限
表示成定积分（ ）
A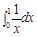． | B． | C． | D． |
B
解析试题分析：由定积分的定义，极限表示成定积分应是，故选B。
考点：本题主要考查定积分的概念。
点评：简单题，定积分“分割、求和、取极限”。
练习册系列答案
相关题目
曲线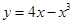
在点（－1，－3）处的切线方程是（ ）
A． | B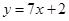． | C． | D． |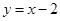
已知函数
与
轴切于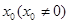
点,且极小值为
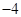,则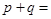
（ ）
| A．12 | B．13 | C．15 | D．16 |
某质点按规律
（
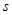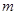单位：
，
单位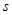：）作变速直线运动，则该质点在
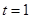时的瞬时速度为（ ）
A．2 | B．3 | C．4 | D．5 |
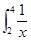dx等于 ( )
| A．-2ln2 | B．2ln2 | C．-ln2 | D．ln2 |
设曲线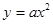
在点（1，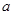
）处的切线与直线
平行，则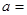
（ ）
| A．1 | B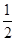． | C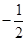． | D． |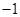
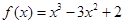在区间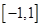
上的最大值是（ ）
| A．-2 | B．0 | C．2 | D．4 |
由直线
，曲线
及
轴所围图形的面积为（ ）
A． | B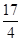． | C． | D． |
是
的导函数，