题目内容
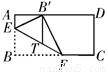
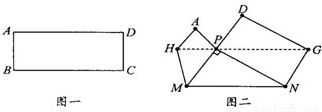
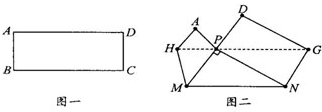把图一的矩形纸片ABCD折叠，B、C两点恰好重合落在AD边上的点P处（如图2），已知∠MPN=90°，PM=3，PN=4，那么矩形纸片ABCD的面积为| 144 |
| 5 |
| 144 |
| 5 |
分析：由勾股定理可求MN，然后可求矩形的宽，最后再利用折叠的性质求出BC的长度，代入矩形的 面积公式可求
解答：解：由勾股定理可得MN=5
设Rt△PMN的斜边上的高为h，则矩形的宽AB也为h
根据直角三角形的面积公式得h=
=
=
由折叠的性质可得，BC=PM+MN+PN=12
矩形的面积公AB•BC=
故答案为：
设Rt△PMN的斜边上的高为h，则矩形的宽AB也为h
根据直角三角形的面积公式得h=
| PM•PN |
| MN |
| 3×4 |
| 5 |
| 12 |
| 5 |
由折叠的性质可得，BC=PM+MN+PN=12
矩形的面积公AB•BC=
| 144 |
| 5 |
故答案为：
| 144 |
| 5 |
点评：本题利用了：折叠的性质：主要思想是一种关于直线的轴对称变换，根据轴对称的性质，及解三角形的基本工具：由勾股定理，及直角三角形和矩形的面积公式求解．
练习册系列答案
阅读快车系列答案
相关题目
）cm2 B．( 
π-
)
π+
）
π+
的角的正切值是 .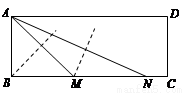
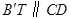交EF于点T，求点T的轨迹方程．
