题目内容
已知函数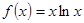 ,
,
(1)求函数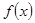 的极值点;
的极值点;
(2)若直线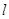 过点
过点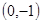 ,并且与曲线
,并且与曲线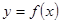 相切,求直线
相切,求直线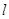 的方程;
的方程;
(3)设函数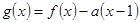 ,其中
,其中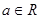 ,求函数
,求函数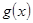 在
在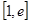 上的最小值(其中
上的最小值(其中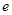 为自然对数的底数).
为自然对数的底数).
【答案】
(1)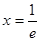 是函数的极小值点,极大值点不存在;(2)
是函数的极小值点,极大值点不存在;(2)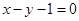 ;(3)当
;(3)当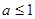 时,
时,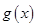 的最小值为0;当
的最小值为0;当 时,
时,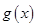 的最小值为
的最小值为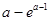 ;当
;当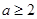 时,
时,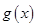 的最小值为
的最小值为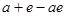 .
.
【解析】
试题分析:(1)先求函数的定义域,再按用导数法求极值的步骤求解;(2)设切点的坐标,用点斜式写出切线的方程,由点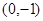 在切线上求出切点的横坐标,从而求得切线的方程;(3).
在切线上求出切点的横坐标,从而求得切线的方程;(3).
试题解析:(1)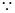
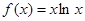 ,
,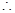
 ,
,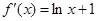 ,令
,令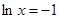 ,则
,则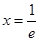 .
.
当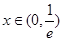 ,
,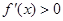 ,
,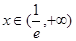 ,
,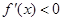 ,故
,故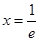 是函数的极小值点,极大值点不存在.
是函数的极小值点,极大值点不存在.
(2)由直线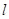 过点
过点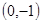 ,并且与曲线
,并且与曲线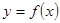 相切,而
相切,而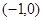 不在
不在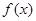 的图象上,
的图象上,
设切点为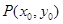 ,
,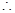 直线
直线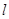 的斜率
的斜率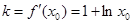 ,方程为
,方程为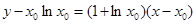 ,
,
又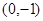 在直线
在直线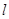 上,
上,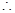
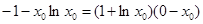 ,解得
,解得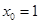 ,
,
故直线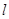 的方程为
的方程为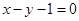 .
.
(3)依题意, ,
,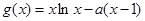 ,
,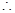
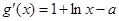 ,令
,令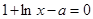 ,则
,则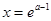 ,
,
所以当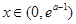 ,
,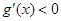 ,
,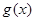 单调递减;
单调递减;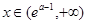 ,
,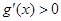 ,
,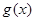 单调递增;
单调递增;
又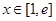 ,所以①当
,所以①当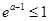 ,即
,即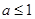 时,
时,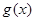 的极小值为
的极小值为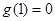 ;②当
;②当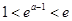 ,即
,即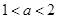 时,
时,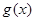 的极小值为
的极小值为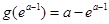 ;③当
;③当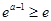 ,即
,即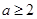 时,
时,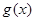 的极小值为
的极小值为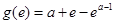 .
.
故①当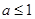 时,
时,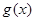 的最小值为0;②当
的最小值为0;②当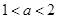 时,
时,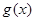 的最小值为
的最小值为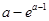 ;③当
;③当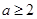 时,
时,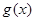 的最小值为
的最小值为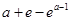 .
.
考点:用导数法求函数的极值,最值.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 .
. 的定义域
;
的定义域
; ,求实数
,求实数 的值.
的值. .
. 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.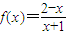 ;
; 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由. 令
令
 的定义域;
的定义域; 的奇偶性,并予以证明;
的奇偶性,并予以证明; ,猜想
,猜想 之间的关系并证明.
之间的关系并证明. ,
, 的定义域;(2)证明:
的定义域;(2)证明: ,求
,求 的取值范围。
的取值范围。