题目内容
 已知函数
已知函数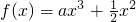 在x=-1处取得极大值,记g(x)
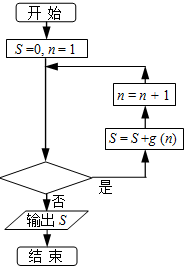
在x=-1处取得极大值,记g(x)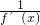 .某程序框图如图所示,若输出的结果S>
.某程序框图如图所示,若输出的结果S> ,则判断框中可以填入的关于n的判断条件是
,则判断框中可以填入的关于n的判断条件是
- A.n≤2011?
- B.n≤2012?
- C.n>2011?
- D.n>2012?
B
分析:由f(x)在x=-1处取得极大值可得f′(-1)=0,由此可求得a值,则g(x)=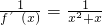 ,g(n)=
,g(n)=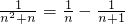 ,输出的结果S=g(1)+g(2)+…+g(n)=1-
,输出的结果S=g(1)+g(2)+…+g(n)=1-
 +…+
+…+ =
= ,令S>
,令S> 可得n>2011,即n=2012时S开始大于
可得n>2011,即n=2012时S开始大于 ,结合选项可得答案.
,结合选项可得答案.
解答:f′(x)=3ax2+x,
因为f(x)在x=-1处取得极大值,
所以f′(-1)=0,即3a-1=0,解得a= ,
,
故f′(x)=x2+x,则g(x)=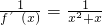 ,
,
g(n)=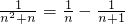 ,
,
该循环结构为当型循环结构,选项C、D显然不正确,
输出的结果S=g(1)+g(2)+…+g(n)=1-
 +…+
+…+ =
= ,
,
由S> ,得
,得 >
> ,解得n>2011,
,解得n>2011,
所以n=2012时S开始大于 ,
,
故判断框中可以填入的关于n的判断条件为:n≤2012?,
故选B.
点评:本题考查函数在某点取得极值的条件及程序框图,考查学生对题目的阅读理解能力及解决问题的能力.
分析:由f(x)在x=-1处取得极大值可得f′(-1)=0,由此可求得a值,则g(x)=
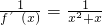 ,g(n)=
,g(n)=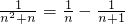 ,输出的结果S=g(1)+g(2)+…+g(n)=1-
,输出的结果S=g(1)+g(2)+…+g(n)=1-
 +…+
+…+ =
= ,令S>
,令S> 可得n>2011,即n=2012时S开始大于
可得n>2011,即n=2012时S开始大于 ,结合选项可得答案.
,结合选项可得答案.解答:f′(x)=3ax2+x,
因为f(x)在x=-1处取得极大值,
所以f′(-1)=0,即3a-1=0,解得a=
 ,
,故f′(x)=x2+x,则g(x)=
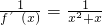 ,
,g(n)=
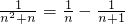 ,
,该循环结构为当型循环结构,选项C、D显然不正确,
输出的结果S=g(1)+g(2)+…+g(n)=1-

 +…+
+…+ =
= ,
,由S>
 ,得
,得 >
> ,解得n>2011,
,解得n>2011,所以n=2012时S开始大于
 ,
,故判断框中可以填入的关于n的判断条件为:n≤2012?,
故选B.
点评:本题考查函数在某点取得极值的条件及程序框图,考查学生对题目的阅读理解能力及解决问题的能力.

练习册系列答案
相关题目
 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量
 的单调区间;
的单调区间;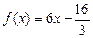 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由. 在x=1处取得极值2,
在x=1处取得极值2,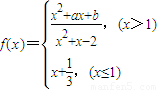 在x=1处连续,则a+b=( )
在x=1处连续,则a+b=( )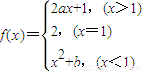 在x=1处连续,则a= ,b= .
在x=1处连续,则a= ,b= . 已知函数
在x=1处取得极值,在x=2处的切线平行于向量
已知函数
在x=1处取得极值,在x=2处的切线平行于向量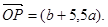
 的单调区间;
的单调区间;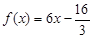 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.