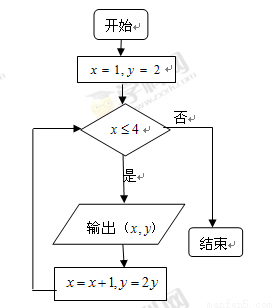
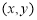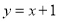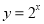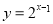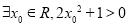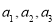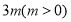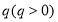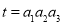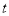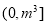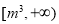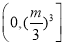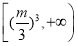题目内容
已知
图像过点
，且在
处的切线方程是
.
（1）求
的解析式；
（2）求在区间
上的最大值和最小值．
（1）
；（2）
，
.
【解析】
试题分析：本试题主要是考查了导数在研究函数中的运用.（1）先由
，计算出
，然后计算出
，根据题中条件可得
即
，求解方程组即可；（2）先求出导数等于零的解，然后确定函数的单调区间与极值点，列出表格，从表格中的极值与端点值，可得函数的最值.
试题解析：（1）
1分
，∴
，∴
3分
又∵切点为
，∴
5分
联立可得
6分
∴
7分
（2）
8分
令
令
或
令
10分
|
|
|
|
| 2 |
| 3 |
|
| ＋ | 0 | － | 0 | ＋ |
|
|
| ↗ | 5 | ↘ |
| ↗ |
|
由上表知，在区间
上，当
时，
当
时，
14分.
考点：1.导数的几何意义；2.函数的最值与导数.
练习册系列答案
相关题目
