Question

如图，在棱长为a的正方体ABCD—A₁B₁C₁D₁中，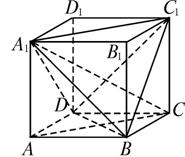

(1)求证：B₁D₁∥面C₁BD；

(2)求证：面AB₁D₁∥面C₁BD；

(3)求证：A₁C⊥面C₁BD；

(4)求证：面C₁BD⊥面ACC₁A₁；

(5)求三棱锥B—A₁C₁D的体积.

Answer 1

解析：(1)如图，在正方体ABCD-A₁B₁C₁D₁中，

AA₁BB₁，AA₁D₁DBB₁D₁D，

∴B₁BDD₁是平行四边形D₁B₁∥BD，

又B₁D₁面C₁BD，BD面C₁BD，∴B₁D₁∥面C₁BD.

(2)由(1)得B₁D₁∥面C₁BD，

同理，同AD₁∥BC₁知AD₁∥面C₁BD，

而AD₁与B₁D₁是面AB₁D₁内两条相交直线，

∴面AB₁D₁∥面C₁BD.

(3)如上图，在正方体ABCD-A₁B₁C₁D₁中，

∵BD⊥AC，且由AA₁⊥面ABCD知∴BD⊥AA₁.

∴BD⊥面ACC₁A₁，又A₁C面ACC₁A₁，∴A₁C⊥BD.

同理A₁C⊥C₁D，∴A₁C⊥面C₁BD.

(4)由(3)得A₁C⊥面C₁BD，A₁C面ACC₁A₁，

∴面C₁BD⊥面ACC₁A.

(5)如上图

.