题目内容
题文已知函数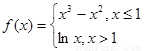 .
.
(1)求函数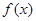 的单调递减区间;
的单调递减区间;
(2)若不等式 对一切
对一切 恒成立,求
恒成立,求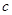 的取值范围.
的取值范围.
【答案】
(1)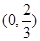 (2)
(2)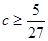
【解析】
试题分析:(1)由于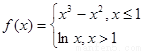 ,
,
当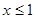 时,
时,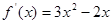 ,令
,令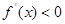 ,可得
,可得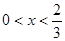 .
.
当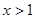 时,
时, 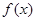 单调递增.
单调递增.
所以函数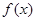 的单调递减区间为
的单调递减区间为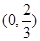 . 4分
. 4分
(2)设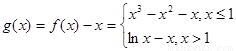 ,
,
当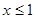 时,
时, 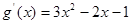 ,
,
令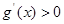 ,可得
,可得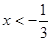 或
或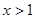 ,即
,即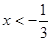
令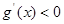 ,可得
,可得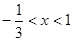 .
.
所以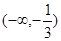 为函数
为函数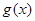 的单调递增区间,
的单调递增区间, 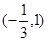 为函数
为函数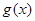 的单调递减区间.
的单调递减区间.
当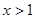 时,
时, 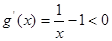 ,可得
,可得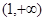 为函数
为函数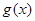 的单调递减区间.
的单调递减区间.
所以函数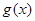 的单调递增区间为
的单调递增区间为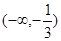 ,单调递减区间为
,单调递减区间为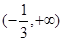 .
.
所以函数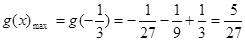 ,
,
要使不等式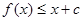 对一切
对一切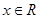 恒成立,即
恒成立,即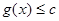 对一切
对一切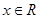 恒成立,
恒成立,
所以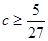 . …12分
. …12分
考点:本小题主要考查导数的计算,单调区间的求解以及恒成立问题的解决。
点评:求分段函数的单调区间时,要注意分段讨论求解,而恒成立问题一般转化为最值问题求解,另外因为此类问题一般以解答题的形式出现,所以一定要注意步骤完整.

练习册系列答案
相关题目
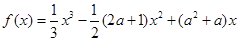 .
.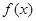 在
在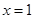 处取得极大值,求实数
处取得极大值,求实数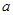 的值;
的值;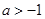 ,求
,求 上的最大值.
上的最大值.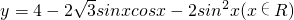 ,
,