题目内容
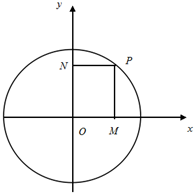 如图,已知P是单位圆(圆心在坐标原点)上一点,∠xOP=
如图,已知P是单位圆(圆心在坐标原点)上一点,∠xOP=| π |
| 3 |
(1)比较|OM|与
| π |
| 6 |
(2)∠AOB的两边交矩形OMPN的边于A,B两点,且∠AOB=
| π |
| 4 |
| OA |
| OB |
分析:(1)记C(0,1),可求
,|OM|,由|PC|<
,可得结论;
(2)设∠AOx=α,α∈[0,
],P(
,
),记f(α)=
•
,分α∈[0,
],α∈(
,
]两种情况进行讨论,表示出f(α),根据其单调性及端点处函数值可求得范围;
 |
| PC |
 |
| PC |
(2)设∠AOx=α,α∈[0,
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| OA |
| OB |
| π |
| 12 |
| π |
| 12 |
| π |
| 4 |
解答:解:(1)记C(0,1),连接PC,则
=
-
=
,
依题意|OM|=|PN|=cos60°<|PC|<
,
∴|OM|<
;
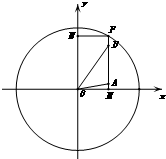
(2)设∠AOx=α,α∈[0,
],P(
,
),记f(α)=
•
,
①当α∈[0,
]时,A(
,
tanα),B(
,
tan(α+
)),
∴f(α)=
•
=
+
tanα•tan(α+
)
=
(1+tanα
)=
•
=
•
=
•
=
•
=
;
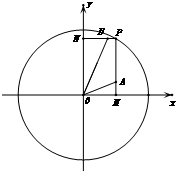
②当α∈(
,
]时,A(
,
tanα),B(
,
),
∴f(α)=
•
=
(
+tanα)
=
(
+tanα)=
•
=
•
=
•
=
•
;
综上,f(α)=
,
f(α)在α∈[0,
]增函数,在α∈(
,
]是减函数,在α∈(
,
]是增函数,
∵f(0)=
,f(
)=
,f(
)=
,f(
)=
,
∴f(α)=
•
∈[
,
].
 |
| PC |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
依题意|OM|=|PN|=cos60°<|PC|<
 |
| PC |
∴|OM|<
| π |
| 6 |

(2)设∠AOx=α,α∈[0,
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| OA |
| OB |
①当α∈[0,
| π |
| 12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
∴f(α)=
| OA |
| OB |
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
=
| 1 |
| 4 |
| 1+tanα |
| 1-tanα |
| 1 |
| 4 |
| 1+tan2α |
| 1-tanα |
=
| 1 |
| 4 |
| 1 |
| cosα(cosα-sinα) |
=
| 1 |
| 4 |
| 1 |
| cos2α-cosαsinα |
| 1 |
| 2 |
| 1 |
| 1+cos2α-sin2α |
=
| 1 | ||||
2(1+
|

②当α∈(
| π |
| 12 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
2tan(α+
|
| ||
| 2 |
∴f(α)=
| OA |
| OB |
| ||
| 4 |
| 1 | ||
tan(α+
|
=
| ||
| 4 |
| 1-tanα |
| 1+tanα |
| ||
| 4 |
| 1+tan2α |
| 1+tanα |
=
| ||
| 4 |
| 1 |
| cosα(cosα+sinα) |
| ||
| 2 |
| 1 |
| 1+cos2α+sin2α |
=
| ||
| 2 |
| 1 | ||||
1+
|
综上,f(α)=
|
f(α)在α∈[0,
| π |
| 12 |
| π |
| 12 |
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
∵f(0)=
| 1 |
| 4 |
| π |
| 12 |
| ||
| 2 |
| π |
| 8 |
| ||||
| 2 |
| π |
| 4 |
| ||
| 4 |
∴f(α)=
| OA |
| OB |
| 1 |
| 4 |
| ||
| 4 |
点评:本题考查三角函数中的恒等变换、平面向量的综合应用,考查分类讨论思想、数形结合思想,考查学生解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B. ,作PM⊥x轴于M,PN⊥y轴于N.
,作PM⊥x轴于M,PN⊥y轴于N.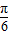 的大小,并说明理由;
的大小,并说明理由;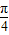 ,求
,求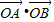 的取值范围.
的取值范围.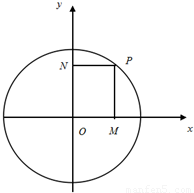
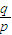 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)
 ,其中p、q均为整数且p、q互质)
,其中p、q均为整数且p、q互质)