题目内容
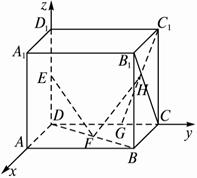
在棱长为1的正方体ABCD—A1B1C1D1中,E、F分别是D1D、BD的中点,G在棱CD上,且CG=(1)求证:EF⊥B1C;
(2)求EF与C1G所成的角的余弦值;
(3)求FH的长.
解:如图,建立空间直角坐标系D—xyz,D为坐标原点,则有E(0,0,![]() )、F(
)、F(![]() ,
,![]() ,0)、C(0,1,0)、C1(0,1,1)、B1(1,1,1)、G(0,
,0)、C(0,1,0)、C1(0,1,1)、B1(1,1,1)、G(0,![]() ,0).
,0).
 ?
?
(1)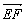 =(
=( ![]() ,
,![]() ,0)-(0,0,
,0)-(0,0, ![]() )=(
)=(![]() ,
,![]() ,-
,-![]() ),?
),?
![]() =(0,1,0)-(1,1,1)=(-1,0,-1),?
=(0,1,0)-(1,1,1)=(-1,0,-1),?
∴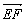 ·
·![]() =
=![]() ×(-1)+
×(-1)+![]() ×0+(-
×0+(-![]() )×(-1)=0,?
)×(-1)=0,?
∴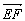 ⊥
⊥![]() ,即EF⊥B1C.?
,即EF⊥B1C.?
(2)∵![]() =(0,
=(0,![]() ,0)-(0,1,1)=(0,-
,0)-(0,1,1)=(0,- ![]() ,-1),?
,-1),?
∴|![]() |=
|=![]() .?
.?
又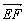 ·
·![]() =
=![]() ×0+
×0+![]() ×(-
×(-![]() )+(-
)+(-![]() )×(-1)=
)×(-1)=![]() ,|
,|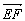 |=
|=![]() ,
,
∴cos〈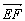 ,
,![]() 〉=
〉= =
=![]() .?
.?
即异面直线EF与C1G所成角的余弦值为![]() .?
.?
(3)∵F(![]() ,
,![]() ,0)、H(0,
,0)、H(0,![]() ,
,![]() ),?
),?
∴![]() =(-
=(-![]() ,
,![]() ,
,![]() ),?
),?
∴|![]() |=
|=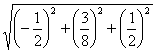 =
=![]() .
.
点评:本题主要是利用空间向量的基础知识,证明异面直线垂直,求异面直线所成的角及线段的长度.应用空间向量的坐标运算解决立体几何问题,使复杂的线面关系的论证、角、距离的计算变得程序化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在线段AD1上运动,给出以下四个命题:
在线段AD1上运动,给出以下四个命题: 在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1 和BB1的中点,那么直线AM与CN所成角的余弦值是( )
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1 和BB1的中点,那么直线AM与CN所成角的余弦值是( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
(2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.