题目内容
(本题12分)
已知函数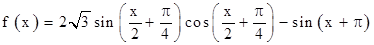 。
。
(1)求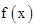 的最小正周期;
的最小正周期;
(2)若将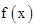 的图象按向量
的图象按向量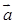 =(
=( ,0)平移得到函数g(x)的图象,求函数g(x)在区间
,0)平移得到函数g(x)的图象,求函数g(x)在区间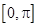 上的最大值和最小值。
上的最大值和最小值。
【答案】
(I) 的最小正周期为;
的最小正周期为;
(Ⅱ)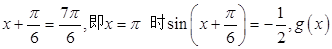 取得最小值—1.
取得最小值—1.
【解析】
试题分析:(1)利用三角函数的恒等变换化简函数解析式,从而求得函数f(x)的最小正周期.(2)将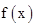 的图象按向量
的图象按向量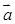 =(
=(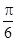 ,0)平移得到函数g(x)的图象,结合三角函数的性质得到最值。
,0)平移得到函数g(x)的图象,结合三角函数的性质得到最值。
解:(I)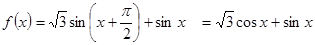 …………………2分
…………………2分
=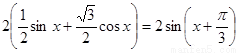 ………………………………4分
………………………………4分
所以 的最小正周期为
的最小正周期为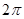 ……………………………5分
……………………………5分
(Ⅱ)∵将 将
将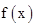 的图象按向量
的图象按向量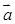 =(
=(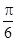 ,0)平移,得到函数
,0)平移,得到函数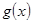 的图象.
的图象.
∴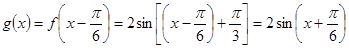 …………………9分
…………………9分
∵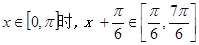 …………………………10分
…………………………10分
∴当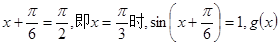 取得最大值2. ……11分
取得最大值2. ……11分
当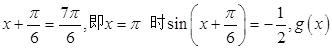 取得最小值—1.…12分
取得最小值—1.…12分
考点:本试题主要考查了三角函数的恒等变换及化简求值,正弦函数的定义域和值域,周期性和单调性,以及三角函数的图象的变换,属于中档题。
点评:解题的关键是对函数解析式的化简,以及对正弦函数的基础知识的熟练记忆。

练习册系列答案
相关题目
 的图像关于原点对称,并且当
的图像关于原点对称,并且当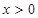 时,
时, ,试求
,试求 上的表达式,并画出它的图像,根据图像写出它的单调区间。
上的表达式,并画出它的图像,根据图像写出它的单调区间。 (1)求
(1)求 的定义域;(2)求
的定义域;(2)求
 关于点
关于点 对称.
对称. 的值.
的值. .
. 时,求函数
时,求函数 的单调递减区间;
的单调递减区间; 时,
时, 上恒大于0,求实数
上恒大于0,求实数 的取值范围.
的取值范围. 的不等式
的不等式 ,其中
,其中 .
. 变化时,试求不等式的解集
变化时,试求不等式的解集 ;
;  (其中
(其中 为整数集). 试探究集合
为整数集). 试探究集合 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合