Question

【题目】已知函数.

（1） 把的图象上每一点的纵坐标变为原来的倍，再将横坐标向右平移 个单位，可得图象，求，的值；

（2） 若对任意实数和任意，恒有，求实数的取值范围.

Answer 1

【答案】（1） ；（2） .

【解析】

（1）由图象变换规律得到，的值；

（2）令m＝3+2sinθcosθ，n＝asinθ+acosθ，则，利用三角函数公式换元，即可得解.

（1）=.

把的图象上每一点的纵坐标变为原来的倍，再将横坐标向右平移 个单位，可得图象，

∴；

（2）任意x∈R与，有恒成立

令m＝3+2sinθcosθ，n＝asinθ+acosθ，则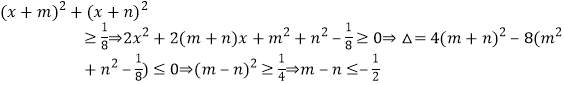或

令t＝sinθ+cosθ2sinθcosθ＝t2﹣1且，

即：m＝t2+2，n＝at，m﹣n＝t2﹣at+2

则：或

参数分离求最值（注意单调区间）

由或

或或

其中在上单调递减，，当且仅当等号成立.

由单调性可得或

综上可得实数a的取值范围为．