题目内容
已知直线l过点(-2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )A.(-2
,2
) B.(- 
,
) C.(-
,
) D.(-
,
)
C
解法一:设直线l的斜率为k,
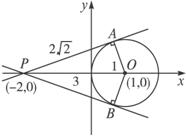
则l的方程为y=k(x+2),由于l与圆x2+y2=2x有两个交点,则d=＜1,
解得-＜k＜.
解法二:kmax=tanα=∴-＜k＜.
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
培优好卷单元加期末卷系列答案
,2
) B.(-
,
) C.(-
,
) D.(-
,
)
,2
) B.(-
,
) C.(-
,
) D.(-
,
)
,2
) B.(-
,
)
,
) D.(-
,
)
,
) B.(-
,
)
,
) D.(-
,
)
,2
) D.(-
)