题目内容
直线 与圆
与圆 相交于A、B两点,若
相交于A、B两点,若 ,则实数t的范围
.
,则实数t的范围
.
【答案】

【解析】
试题分析:方法一:将直线 代入圆的方程得
代入圆的方程得 ,因为交与A、B两点,则
,因为交与A、B两点,则 ,即
,即 ,设
,设 ,故
,故
 ,
, =
= ,则
,则 >
> ,两边平方且
,两边平方且 ,代入解得
,代入解得 ,∴
,∴ ,故
,故 的取值范围是
的取值范围是 .
.

方法二:∵直线tx+y+3=0与圆x2+y2=4交于相异两点A、B,∴O点到直线tx+y+3=0的距离d<2,又因为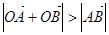 ,由平行四边形可知,夹角为钝角的邻边所对的对角线比夹角为锐角的邻边所对的对角线短,
,由平行四边形可知,夹角为钝角的邻边所对的对角线比夹角为锐角的邻边所对的对角线短, 的夹角为锐角,圆心到直线的距离d大于
的夹角为锐角,圆心到直线的距离d大于 ,故
,故 ,即
,即
 ,解之得
,解之得 的取值范围是
的取值范围是 .
.
考点:1、直线和圆的位置关系;2、向量的模.

练习册系列答案
相关题目
 ,过点P的直线
,过点P的直线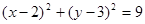 相交于A,B两点,则|AB|的最小值为(
)
相交于A,B两点,则|AB|的最小值为(
)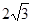 B.4 C.
B.4 C.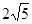 D.5
D.5 与圆
与圆 相交于A、B两点,则
相交于A、B两点,则 ▲
。
▲
。  与圆
与圆 相交于A、B两点,若
相交于A、B两点,若 ,则实数t的范围
,则实数t的范围
 与圆
与圆 相交于A、B两点,则
相交于A、B两点,则 ▲ .
▲ .