题目内容
在△ABC中,已知 ,
, ,则cosC的值为( )
,则cosC的值为( )A.

B.

C.
 或
或
D.

【答案】分析:在三角形中根据所给A和B角的三角函数值,求出A的正弦值和B的余弦值,根据A+B+C=180°,用诱导公式求出C的余弦值,解题过程中注意B的余弦值有两个,根据条件舍去不合题意的.
解答:解:∵cosA=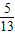 ,A∈(0,π),
,A∈(0,π),
∴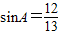 ,
,
∵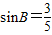 ,B∈(0,π),
,B∈(0,π),
∴cosB=± ,
,
当∠B是钝角时,A与B两角的和大于π,
∴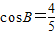 ,
,
∴cosC=-cos(A+B)=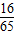 ,
,
故选A
点评:本题借助于三角形内角的关系,用诱导公式和同角三角函数之间的关系解决问题,本题是一个易错题,易错的地方是角B的余弦值,解题时往往忽略三角形内角和而盲目解题.
解答:解:∵cosA=
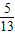 ,A∈(0,π),
,A∈(0,π),∴
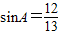 ,
,∵
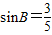 ,B∈(0,π),
,B∈(0,π),∴cosB=±
 ,
,当∠B是钝角时,A与B两角的和大于π,
∴
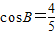 ,
,∴cosC=-cos(A+B)=
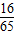 ,
,故选A
点评:本题借助于三角形内角的关系,用诱导公式和同角三角函数之间的关系解决问题,本题是一个易错题,易错的地方是角B的余弦值,解题时往往忽略三角形内角和而盲目解题.

练习册系列答案
相关题目