题目内容
|
（本小题满分12分） 设为实数，函数,. （Ⅰ）求的单调区间与极值； （Ⅱ）求证：当且时，. （本小题满分12分） （Ⅰ）解：由知。 …………………2分 令，得。于是，当变化时，和的变化情况如下表：
……………………………4分 故的单调递减区间是，单调递增区间是。在处取得极小值。极小值为 …………………6分 （Ⅱ）证明：设，于是。 由（Ⅰ）知当时取最小值为 于是对任意,都有，所以在R内单调递增。 …………8分 于是，当时，对任意，都有，而 …………10分 从而对任意，都有。即故…12分 
练习册系列答案
 阅读快车系列答案
相关题目
|
（Ⅱ）．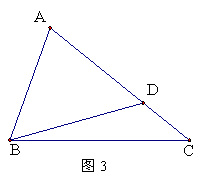
如图3，中，点在线段上，且