题目内容

计算：
（1）已知 a3x=
1
27
，求 
a2x+a-2x
ax+a-x
的值．
（2）
log
81
2
3
-
log
16
2
3
+
log
20
2
3
-
log
30
2
3
．
分析：（1）先根据已知条件得出ax=
1
3
，然后将所求的式子化简为
(ax)2+
1
(ax)2
ax+
1
ax
，最后将值代入即可．
（2）直接根据对数的运算性质解答即可．
解答：解：（1）∵a3x=
1
27
，
∴ax=
1
3

 
a2x+a-2x
ax+a-x
=
(ax)2+
1
(ax)2
ax+
1
ax
=
(
1
3
)2+
1
(
1
3
)2
1
3
+3
=
82
9
10
3
=
41
15

（2））
log
81
2
3
-
log
16
2
3
+
log
20
2
3
-
log
30
2
3

=(log
2
3
81-log
2
3
30)-(log
2
3
16-log
2
3
20)
=log
2
3
27
10
-log
2
3
4
5
=log
2
3
27
8

=log
2
3
(
2
3
)-3
=-3
点评：此题考查了对数的运算性质以及有理数指数幂的化简求值，熟练掌握公式是关键，属于中档题．
练习册系列答案
相关题目
计算：（1）已知a-a-1=1，求
a2+a-2-3a4-a-4
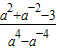的值．
（2）（lg5）2+lg2•lg50的值．
计算：（1）已知a＞0，a2x=3，求
a3x+a-3x
ax+a-x
的值；
（2）求
lg8+lg125-lg2-lg5
lg
10
•lg0.1
的值．
计算：
（1）已知a-a-1=1，求a2+a-2+3的值．
（2）计算log2(23×45)．
计算：（1）已知a-a-1=1，求
a2+a-2-3a4-a-4
的值．
（2）（lg2）3+3lg2•lg5+（lg5）3的值．
计算：（1）已知a-a-1=1，求的值．
（2）（lg2）3+3lg2•lg5+（lg5）3的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网