题目内容
在如图所示的几何体中,四边形 是正方形,
是正方形, 平面
平面 ,
, ,
, 分别为
分别为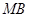 ,
, 的中点,且
的中点,且 .
.

(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求三棱锥 与四棱锥
与四棱锥 的体积之比.
的体积之比.
 是正方形,
是正方形, 平面
平面 ,
, ,
, 分别为
分别为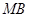 ,
, 的中点,且
的中点,且 .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)求三棱锥
 与四棱锥
与四棱锥 的体积之比.
的体积之比.(Ⅰ)见解析;(Ⅱ) .
.
 .
.试题分析:(Ⅰ)要证面面垂直则先证线面垂直,此题由已知条件先证明
 ,再由在三角形
,再由在三角形 中,
中, ,得
,得 ,从而
,从而 ,易知
,易知 ;(Ⅱ)根据题意易知四棱锥体积,三棱锥
;(Ⅱ)根据题意易知四棱锥体积,三棱锥 可以把
可以把 作为底面,
作为底面, 即为高,可得体积比.
即为高,可得体积比.试题解析:(Ⅰ)

 ,
, 平面
平面 ,
,又
 平面
平面 ,
, ,
, ,
, 又
又 , 4分
, 4分在
 ,
, ,
, ,又
,又 . 6分
. 6分(Ⅱ)
 ,则
,则 ,
, , 8分
, 8分依题意知
 ,
, ,
,
 . 12分
. 12分
练习册系列答案
相关题目
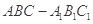 中,
中,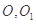 分别是上、下底面的中心.已知
分别是上、下底面的中心.已知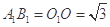 ,
,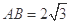 .
.
 的侧棱垂直于底面,各项点都在同一球面上,若
的侧棱垂直于底面,各项点都在同一球面上,若 ,
, ,
, ,
, ,则此球的表面积等于 .
,则此球的表面积等于 . ,则这个正方体的棱长是( )
,则这个正方体的棱长是( )



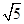 ,球面上有A、B、C三点,如果
,球面上有A、B、C三点,如果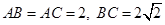 ,则三棱锥O-ABC 的体积为 ( )
,则三棱锥O-ABC 的体积为 ( )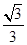 (B)
(B)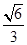 (C)1 (D)
(C)1 (D)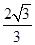




 ,求其直径
,求其直径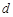 的一个近似公式
的一个近似公式 . 人们还用过一些类似的近似公式. 根据
. 人们还用过一些类似的近似公式. 根据 判断,下列近似公式中最精确的一个是( )
判断,下列近似公式中最精确的一个是( )


 中,已知
中,已知 是边长为1的正方形,且
是边长为1的正方形,且 是正三角形,,
是正三角形,, ,则该多面体的体积为( )
,则该多面体的体积为( )



