题目内容
给出以下命题:
①不等式|2x-1|>3的解集是{x|x>2};
②若直线ax+by=4与圆x2+y2=4没有公共点,则点(a,b)一定在圆x2+y2=4外;
③“?x0∈R,使得ax02+(a-3)x0+1≤0”是假命题,则1<a<9;
④某人向一个圆内投镖,则镖扎到该圆的内接正三角形区域内的概率为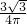 .其中正确命题的序号是________.
.其中正确命题的序号是________.
③④
分析:①解出不等式|2x-1|>3的解集为{x|x>2或x<-1}.②因为直线ax+by=4与圆x2+y2=4没有公共点,计算出圆心到直线的距离并且与半径比较大小,进而整理可得a2+b2<4,所以点(a,b)一定在圆x2+y2=4内.③由题意可得不等式ax2+(a-3)x+1>0恒成立,即1<a<9.④设圆的半径为r,内接正三角形的边长为a,则a= r,分别计算出三角形与圆的面积,再根据几何概率模型可得④正确.
r,分别计算出三角形与圆的面积,再根据几何概率模型可得④正确.
解答:①因为不等式为|2x-1|>3,所以2x-1>3或2x-1<-3,解得x>2或x<-1,所以原不等式的解集为{x|x>2或x<-1}.所以①错误.
②因为直线ax+by=4与圆x2+y2=4没有公共点,所以圆心到直线的距离 >2=r,整理可得a2+b2<4,所以点(a,b)一定在圆x2+y2=4内,所以②错误.
>2=r,整理可得a2+b2<4,所以点(a,b)一定在圆x2+y2=4内,所以②错误.
③因为“?x0∈R,使得ax02+(a-3)x0+1≤0”是假命题,所以不等式ax2+(a-3)x+1>0恒成立,即1<a<9,所以③正确.
④设圆的半径为r,内接正三角形的边长为a,则a= r,所以内接正三角形的面积为
r,所以内接正三角形的面积为 ,圆的面积为πr2,根据几何概率模型可得所以镖扎到该圆的内接正三角形区域内的概率为
,圆的面积为πr2,根据几何概率模型可得所以镖扎到该圆的内接正三角形区域内的概率为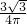 ,所以④正确.
,所以④正确.
故答案为:③④.
点评:解决此类问题的关键是熟练掌握基础知识,即解含绝对值的不等式,恒成立问题,存在性命题与几何概率模型等知识点.
分析:①解出不等式|2x-1|>3的解集为{x|x>2或x<-1}.②因为直线ax+by=4与圆x2+y2=4没有公共点,计算出圆心到直线的距离并且与半径比较大小,进而整理可得a2+b2<4,所以点(a,b)一定在圆x2+y2=4内.③由题意可得不等式ax2+(a-3)x+1>0恒成立,即1<a<9.④设圆的半径为r,内接正三角形的边长为a,则a=
 r,分别计算出三角形与圆的面积,再根据几何概率模型可得④正确.
r,分别计算出三角形与圆的面积,再根据几何概率模型可得④正确.解答:①因为不等式为|2x-1|>3,所以2x-1>3或2x-1<-3,解得x>2或x<-1,所以原不等式的解集为{x|x>2或x<-1}.所以①错误.
②因为直线ax+by=4与圆x2+y2=4没有公共点,所以圆心到直线的距离
 >2=r,整理可得a2+b2<4,所以点(a,b)一定在圆x2+y2=4内,所以②错误.
>2=r,整理可得a2+b2<4,所以点(a,b)一定在圆x2+y2=4内,所以②错误.③因为“?x0∈R,使得ax02+(a-3)x0+1≤0”是假命题,所以不等式ax2+(a-3)x+1>0恒成立,即1<a<9,所以③正确.
④设圆的半径为r,内接正三角形的边长为a,则a=
 r,所以内接正三角形的面积为
r,所以内接正三角形的面积为 ,圆的面积为πr2,根据几何概率模型可得所以镖扎到该圆的内接正三角形区域内的概率为
,圆的面积为πr2,根据几何概率模型可得所以镖扎到该圆的内接正三角形区域内的概率为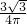 ,所以④正确.
,所以④正确.故答案为:③④.
点评:解决此类问题的关键是熟练掌握基础知识,即解含绝对值的不等式,恒成立问题,存在性命题与几何概率模型等知识点.

练习册系列答案
相关题目
 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题; ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;