题目内容
函数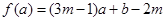 ,当
,当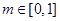 时,
时,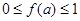 恒成立, 则
恒成立, 则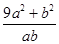 的最大值与最小值之和为( )
的最大值与最小值之和为( )
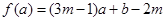 ,当
,当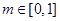 时,
时,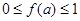 恒成立, 则
恒成立, 则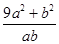 的最大值与最小值之和为( )
的最大值与最小值之和为( )| A.18 | B.16 | C.14 | D.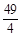 |
B
令 ,因为当
,因为当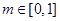 时,
时,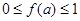 恒成立,即
恒成立,即 恒成立,所以
恒成立,所以 ,即
,即
满足上述条件的点 的可行域如下:
的可行域如下:

由图可知,目标函数 在边界
在边界 上取到最小值1,在点
上取到最小值1,在点 处取到最大值4,所以
处取到最大值4,所以
而 ,令
,令 ,则
,则
 ,
, ,当
,当 时,
时, ,此时函数
,此时函数 单调递减,当
单调递减,当 时,
时, ,此时函数
,此时函数 单调递增
单调递增
所以函数 在点
在点 处取到最小值6,因为
处取到最小值6,因为 时
时 ,
, 时
时
所以函数 在点
在点 处取到最大值10
处取到最大值10
所以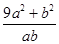 的最小值为6,最大值为10,则两者之和为16,故选B
的最小值为6,最大值为10,则两者之和为16,故选B
 ,因为当
,因为当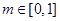 时,
时,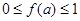 恒成立,即
恒成立,即 恒成立,所以
恒成立,所以 ,即
,即
满足上述条件的点
 的可行域如下:
的可行域如下:
由图可知,目标函数
 在边界
在边界 上取到最小值1,在点
上取到最小值1,在点 处取到最大值4,所以
处取到最大值4,所以
而
 ,令
,令 ,则
,则
 ,
, ,当
,当 时,
时, ,此时函数
,此时函数 单调递减,当
单调递减,当 时,
时, ,此时函数
,此时函数 单调递增
单调递增所以函数
 在点
在点 处取到最小值6,因为
处取到最小值6,因为 时
时 ,
, 时
时
所以函数
 在点
在点 处取到最大值10
处取到最大值10所以
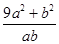 的最小值为6,最大值为10,则两者之和为16,故选B
的最小值为6,最大值为10,则两者之和为16,故选B
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
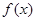 对任意实数
对任意实数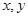 满足:
满足: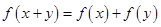 ,且
,且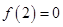 ,则下列结论正确的是_____________.
,则下列结论正确的是_____________.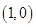 对称;④
对称;④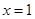 对称.
对称. 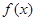 是定义域为R,又
是定义域为R,又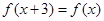 ,当
,当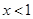 时,
时,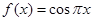
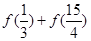 值为( )
值为( )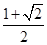
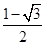
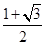
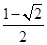
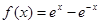 ,
,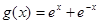
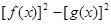 的值;
的值;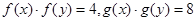 ,求
,求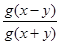 的值。
的值。 是
是 的导函数,
的导函数,
 -bx+3,且f(0)=f(4)。
-bx+3,且f(0)=f(4)。 且
且 则
则 ( )
( )


