题目内容
已知椭圆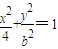 (0<b<2)与y轴交于A、B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( )
(0<b<2)与y轴交于A、B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为( )A.1
B.2
C.4
D.8
【答案】分析:欲求△ABF面积的最大值,先利用椭圆的参数b,c表示出△ABF面积,利用椭圆的参数b,c间的关系消去一个参数,再结合基本不等式求其最大值即可.
解答:解:∵已知椭圆 (0<b<2)
(0<b<2)
∴a=2,c=
则△ABF面积S= AB×OF=
AB×OF= 2b×c
2b×c
=b

当且仅当b= 取等号.
取等号.
则△ABF面积的最大值为2
故选B.
点评:本题主要考查椭圆的基本性质的应用和三角形面积的最大值问题.直线与圆锥曲线的综合题是高考的重点也是热点问题,每年必考,一定要好好准备.解答的关键是基本不等式的应用.
解答:解:∵已知椭圆
 (0<b<2)
(0<b<2)∴a=2,c=

则△ABF面积S=
 AB×OF=
AB×OF= 2b×c
2b×c=b


当且仅当b=
 取等号.
取等号.则△ABF面积的最大值为2
故选B.
点评:本题主要考查椭圆的基本性质的应用和三角形面积的最大值问题.直线与圆锥曲线的综合题是高考的重点也是热点问题,每年必考,一定要好好准备.解答的关键是基本不等式的应用.

练习册系列答案
相关题目
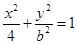 (0<b<2)的离心率等于
(0<b<2)的离心率等于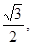 抛物线
抛物线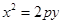 (p>0).
(p>0).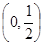 ,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足
,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足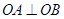 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由. ,其中常数
,其中常数 ;(1)讨论
;(1)讨论 的单调性;(2)若
的单调性;(2)若 ,当
,当 ,
, 恒成立,求
恒成立,求 的取值范围。
的取值范围。 (0<b<2)的离心率等于
(0<b<2)的离心率等于 抛物线
抛物线 (p>0).
(p>0). ,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足
,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.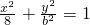 (0<b<2
(0<b<2 )的左、右焦点分别为F1和F2,以F1、F2为直径的圆经过点M(0,b).
)的左、右焦点分别为F1和F2,以F1、F2为直径的圆经过点M(0,b). =0.求证:直线l在y轴上的截距为定值.
=0.求证:直线l在y轴上的截距为定值.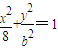 (0<b<2
(0<b<2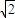 )的左、右焦点分别为F1和F2,以F1、F2为直径的圆经过点M(0,b).
)的左、右焦点分别为F1和F2,以F1、F2为直径的圆经过点M(0,b).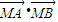 =0.求证:直线l在y轴上的截距为定值.
=0.求证:直线l在y轴上的截距为定值.