题目内容
已知定理:“如果两个非零向量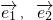 不平行,那么
不平行,那么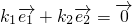 (k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题:
(k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题:
设非零向量 与
与 不平行.已知向量
不平行.已知向量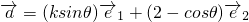 ,向量
,向量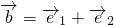 ,且
,且 .求k与θ的关系式;并当θ∈R时,求k的取值范围.
.求k与θ的关系式;并当θ∈R时,求k的取值范围.
解:∵ ,∴存在唯一实数λ,使
,∴存在唯一实数λ,使 ,即
,即
∵ ,
, ,
,
∴
即
∴ksinθ+λ=0,2-cosθ+λ=0
∴ksinθ=2-cosθ,k=
∵ 可看作点(-sinθ,cosθ),与点(0,2)连线的斜率
可看作点(-sinθ,cosθ),与点(0,2)连线的斜率
(-sinθ,cosθ)是圆x2+y2=1上动点,(0.2)是定点
求过(0,2)点的圆的切线斜率,可得k=±
∴- <k<
<k<
答:k与θ的关系式为k= ,当θ∈R时,k的取值范围为(-
,当θ∈R时,k的取值范围为(- ,
, )
)
分析:因为 ,可根据向量平行的充要条件,找到
,可根据向量平行的充要条件,找到 坐标之间的关系,再根据题目中给出的定理,化简,即可得到k与θ的关系式,把关系式看作过定点与动点的直线的斜率,利用直线与圆相切的判断,求出k的范围即可.
坐标之间的关系,再根据题目中给出的定理,化简,即可得到k与θ的关系式,把关系式看作过定点与动点的直线的斜率,利用直线与圆相切的判断,求出k的范围即可.
点评:本题主要考查了利用新概念解题,以及应用直线的斜率公式求范围,考查了学生具有自主学习的能力和转化的思想.
 ,∴存在唯一实数λ,使
,∴存在唯一实数λ,使 ,即
,即
∵
 ,
, ,
,∴

即

∴ksinθ+λ=0,2-cosθ+λ=0
∴ksinθ=2-cosθ,k=

∵
 可看作点(-sinθ,cosθ),与点(0,2)连线的斜率
可看作点(-sinθ,cosθ),与点(0,2)连线的斜率(-sinθ,cosθ)是圆x2+y2=1上动点,(0.2)是定点
求过(0,2)点的圆的切线斜率,可得k=±

∴-
 <k<
<k<
答:k与θ的关系式为k=
 ,当θ∈R时,k的取值范围为(-
,当θ∈R时,k的取值范围为(- ,
, )
)分析:因为
 ,可根据向量平行的充要条件,找到
,可根据向量平行的充要条件,找到 坐标之间的关系,再根据题目中给出的定理,化简,即可得到k与θ的关系式,把关系式看作过定点与动点的直线的斜率,利用直线与圆相切的判断,求出k的范围即可.
坐标之间的关系,再根据题目中给出的定理,化简,即可得到k与θ的关系式,把关系式看作过定点与动点的直线的斜率,利用直线与圆相切的判断,求出k的范围即可.点评:本题主要考查了利用新概念解题,以及应用直线的斜率公式求范围,考查了学生具有自主学习的能力和转化的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
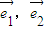 不平行,那么
不平行,那么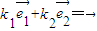 (k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题:
(k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题: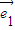 与
与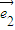 不平行.已知向量
不平行.已知向量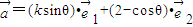 ,向量
,向量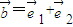 ,且
,且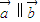 .求k与θ的关系式;并当θ∈R时,求k的取值范围.
.求k与θ的关系式;并当θ∈R时,求k的取值范围.