题目内容
若 ,且
,且 ,,则函数
,,则函数 的单调递增区间是_____________;
的单调递增区间是_____________;
 ,且
,且 ,,则函数
,,则函数 的单调递增区间是_____________;
的单调递增区间是_____________;
试题分析:根据二次函数的对称轴性质,可知函数值相等的两个变量关于对称轴
 对称同时利用
对称同时利用 ,说明了函数与坐标轴的交点横坐标为1和2,因此那么可知
,说明了函数与坐标轴的交点横坐标为1和2,因此那么可知 ,展开可知b=3,c=2,因此
,展开可知b=3,c=2,因此 ,结合绝对值函数的性质,可知在
,结合绝对值函数的性质,可知在 区间上递增,故答案为
区间上递增,故答案为 。
。点评:解决该试题的关键是理解函数的关系式,表示的含义,从而得到参数b的值,进而得到解析式,然后利用分段函数的单调性来确定出单调区间即可。属于基础题。

练习册系列答案
相关题目
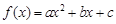 , 满足
, 满足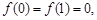 且
且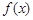 的最小值是
的最小值是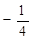 .(Ⅰ)求
.(Ⅰ)求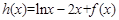 ,若函数
,若函数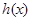 在区间
在区间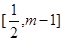 上是单调函数,求实数
上是单调函数,求实数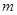 的取值范围。
的取值范围。 ABC的三个内角,且
ABC的三个内角,且 是方程
是方程 的两个实数根,则
的两个实数根,则 在
在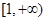 单调递增,则
单调递增,则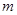 的取值范围为 。
的取值范围为 。 与
与 的图象的交点组成的集合是( )
的图象的交点组成的集合是( )



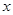 的方程
的方程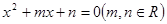 的一个根是
的一个根是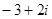 ,则
,则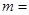 _________.
_________. ,
, ,
, ,
, ,
,




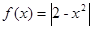 ,若
,若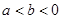 ,且
,且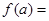
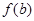 ,则
,则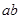 的取值范围是
的取值范围是