题目内容
不等式| x+4 |
分析：此题要注意x+4≥0，2-2x＞0，先对不等式两边平方，然后再移项化成一般式，求出不等式的解集即可．
解答：解：∵
＜2-2x，
∴x+4≥0，2-2x＞0，
∴-4≤x＜1，
∵不等式
＜2-2x，两边平方得，
x+4＜4x2-8x+4，
∴2x2-4x＞0，
解得，x＞
，或x＜0，
∵-4≤x＜1，
∴-4≤x＜0，
∴综上得：不等式的解集为[-4，0）
故答案为[-4，0）．
| x+4 |
∴x+4≥0，2-2x＞0，
∴-4≤x＜1，
∵不等式
| x+4 |
x+4＜4x2-8x+4，
∴2x2-4x＞0，
解得，x＞
| 9 |
| 4 |
∵-4≤x＜1，
∴-4≤x＜0，
∴综上得：不等式的解集为[-4，0）
故答案为[-4，0）．
点评：此题要注意根号有意义的条件，很多学生忽略了这一点，从而导致出错．
练习册系列答案
名校课堂系列答案
相关题目
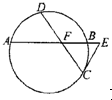选做题：（考生可以在以下三个题任选一道题作答，如果多做以考生所作的第一道题为准）