题目内容
 选做题:(考生可以在以下三个题任选一道题作答,如果多做以考生所作的第一道题为准)
选做题:(考生可以在以下三个题任选一道题作答,如果多做以考生所作的第一道题为准)(a) 不等式|x-4|-|x-2|>1的解集为
(-∞,
)
| 5 |
| 2 |
(-∞,
)
.| 5 |
| 2 |
(b) 已知直线l的极坐标方程为:ρcosθ-ρsinθ-
| 2 |
|
相切
相切
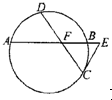
.(c) 如图已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=
| 2 |
| ||
| 2 |
| ||
| 2 |
分析:(a)先对x进行分类讨论,根据x的范围先去掉绝对值然后再根据绝对值不等式的解法进行求解.
(b)先利用sin2θ+cos2θ=1将圆的参数方程化成圆的普通方程,然后利用利用ρcosθ=x,ρsinθ=y,将直线的极坐标方程化成普通方程,最后计算圆心到直线的距离与半径进行比较即可判定位置关系.
(c)设出AF=4k,BF=2k,BE=k,由DF•FC=AF•BF求出k的值,利用切割定理求出CE.
(b)先利用sin2θ+cos2θ=1将圆的参数方程化成圆的普通方程,然后利用利用ρcosθ=x,ρsinθ=y,将直线的极坐标方程化成普通方程,最后计算圆心到直线的距离与半径进行比较即可判定位置关系.
(c)设出AF=4k,BF=2k,BE=k,由DF•FC=AF•BF求出k的值,利用切割定理求出CE.
解答:解:(a)原不等式|x-4|-|x-2|>1.
当x<2时,原不等式化为4-x-(2-x)>1,即2>1,∴x<2;
当2≤x≤4时,原不等式化为4-x-(x-2)>1,∴2≤x<
;
当x>4时,原不等式化为(x-4)-(x-2)>1,即-2>1,∴x∈∅.
综上,原不等式解集为(-∞,
).
故答案为:(-∞,
).
(b)圆的参数方程
(θ为参数),
∴圆的普通方程为x2+y2=1,
直线的极坐标方程为ρcosθ-ρsinθ-
=0,
∴直线的普通方程为x-y-
=0
而d=
=1=r,
∴直线与圆的位置关系是相切.
故答案为:相切.
(c)设AF=4k,BF=2k,BE=k,由DF•FC=AF•BF,得2=8k2,即k=
,
∴AF=2,BF=1,BE=
,AE=
,
由切割定理得CE2=BE•EA=
×
=
∴CE=
.
故答案为:
.
当x<2时,原不等式化为4-x-(2-x)>1,即2>1,∴x<2;
当2≤x≤4时,原不等式化为4-x-(x-2)>1,∴2≤x<
| 5 |
| 2 |
当x>4时,原不等式化为(x-4)-(x-2)>1,即-2>1,∴x∈∅.
综上,原不等式解集为(-∞,
| 5 |
| 2 |
故答案为:(-∞,
| 5 |
| 2 |
(b)圆的参数方程
|
∴圆的普通方程为x2+y2=1,
直线的极坐标方程为ρcosθ-ρsinθ-
| 2 |
∴直线的普通方程为x-y-
| 2 |
而d=
|-
| ||
|
∴直线与圆的位置关系是相切.
故答案为:相切.
(c)设AF=4k,BF=2k,BE=k,由DF•FC=AF•BF,得2=8k2,即k=
| 1 |
| 2 |
∴AF=2,BF=1,BE=
| 1 |
| 2 |
| 7 |
| 2 |
由切割定理得CE2=BE•EA=
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 4 |
∴CE=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:(a)此小题考查绝对值不等式的解法,运用了分类讨论的思想,解题的关键是去掉绝对值,此类题目是高考常见的题型.
(b)本小题主要考查圆的参数方程及直线与圆的位置关系的判断,以及转化与化归的思想方法,属于基础题.
(c)本题是基础题,考查直线与圆的位置关系,考查计算能力,基本知识掌握的情况,常考题型.
(b)本小题主要考查圆的参数方程及直线与圆的位置关系的判断,以及转化与化归的思想方法,属于基础题.
(c)本题是基础题,考查直线与圆的位置关系,考查计算能力,基本知识掌握的情况,常考题型.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 的数学期望。
的数学期望。 ,有1道题答对的概率为
,有1道题答对的概率为 ,还有1道答对的概率为
,还有1道答对的概率为 ,
,









 选做题:(考生可以在以下三个题任选一道题作答,如果多做以考生所作的第一道题为准)
选做题:(考生可以在以下三个题任选一道题作答,如果多做以考生所作的第一道题为准) ,圆C的参数方程为
,圆C的参数方程为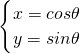 (θ为参数),那么直线l与圆C的位置关系为________.
(θ为参数),那么直线l与圆C的位置关系为________. .若CE与圆相切,则CE的长为________.
.若CE与圆相切,则CE的长为________. ,圆C的参数方程为
,圆C的参数方程为 (θ为参数),那么直线l与圆C的位置关系为 .
(θ为参数),那么直线l与圆C的位置关系为 . .若CE与圆相切,则CE的长为 .
.若CE与圆相切,则CE的长为 .