题目内容
函数f(x)定义域为R,x、y∈R时恒有f(xy)=f(x)+f(y),若f(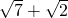 )+f(
)+f(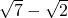 )=2,则f(
)=2,则f(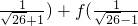 )=________.
)=________.
-4
分析:由已知中x、y∈R时恒有f(xy)=f(x)+f(y),可由f(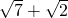 )+f(
)+f(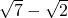 )=2,得到f(5)=2,进而求出f(
)=2,得到f(5)=2,进而求出f( )=-2,进而得到答案.
)=-2,进而得到答案.
解答:∵x、y∈R时恒有f(xy)=f(x)+f(y),
∴令x=y=1,有f(1)=0,
∵f(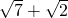 )+f(
)+f(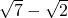 )=f[(
)=f[(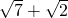 )•(
)•(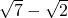 )]=f(5)=2
)]=f(5)=2
取x=5,y= ,得f(1)=f(5•
,得f(1)=f(5• )=f(5)+f(
)=f(5)+f( ),
),
∴f( )=-f(5)=-2
)=-f(5)=-2
∴f( )+f(
)+f( )=f(
)=f( •
• )=f(
)=f( )=f(
)=f( •
• )=2f(
)=2f( )=-4
)=-4
故答案为:-4
点评:本题考查的知识点是抽象函数的应用,函数的值,其中抽象函数解答时,要注意根据已知和未知“凑”出变形方向.
分析:由已知中x、y∈R时恒有f(xy)=f(x)+f(y),可由f(
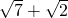 )+f(
)+f(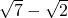 )=2,得到f(5)=2,进而求出f(
)=2,得到f(5)=2,进而求出f( )=-2,进而得到答案.
)=-2,进而得到答案.解答:∵x、y∈R时恒有f(xy)=f(x)+f(y),
∴令x=y=1,有f(1)=0,
∵f(
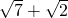 )+f(
)+f(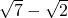 )=f[(
)=f[(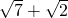 )•(
)•(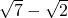 )]=f(5)=2
)]=f(5)=2取x=5,y=
 ,得f(1)=f(5•
,得f(1)=f(5• )=f(5)+f(
)=f(5)+f( ),
),∴f(
 )=-f(5)=-2
)=-f(5)=-2∴f(
 )+f(
)+f( )=f(
)=f( •
• )=f(
)=f( )=f(
)=f( •
• )=2f(
)=2f( )=-4
)=-4故答案为:-4
点评:本题考查的知识点是抽象函数的应用,函数的值,其中抽象函数解答时,要注意根据已知和未知“凑”出变形方向.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目