题目内容
【题目】已知抛物线![]() 的焦点
的焦点![]() 也是椭圆
也是椭圆![]() 的一个焦点,
的一个焦点,![]() 与
与![]() 的公共弦的长为
的公共弦的长为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,与
两点,与![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() 与
与![]() 同向
同向
(ⅰ)若![]() ,求直线
,求直线![]() 的斜率
的斜率
(ⅱ)设![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴的交点为
轴的交点为![]() ,证明:直线
,证明:直线![]() 绕点
绕点![]() 旋转时,
旋转时,![]() 总是钝角三角形
总是钝角三角形
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ,(ii)详见解析.
,(ii)详见解析.
【解析】
试题分析:(1)根据已知条件可求得![]() 的焦点坐标为
的焦点坐标为![]() ,再利用公共弦长为
,再利用公共弦长为![]() 即可求解;(2)(i)设直线
即可求解;(2)(i)设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,由
,由![]() 得
得![]() ,根据条件可知
,根据条件可知![]()
![]() ,从而可以建立关于
,从而可以建立关于![]() 的方程,即可求解;(ii)根据条件可说明
的方程,即可求解;(ii)根据条件可说明![]()
![]()
![]() ,因此
,因此![]() 是锐角,从而
是锐角,从而![]() 是钝角,即可得证
是钝角,即可得证
试题解析:(1)由![]() :
:![]() 知其焦点
知其焦点![]() 的坐标为
的坐标为![]() ,∵
,∵![]() 也是椭圆
也是椭圆![]() 的一焦点,
的一焦点,
∴ ![]() ①,又
①,又![]() 与
与![]() 的公共弦的长为
的公共弦的长为![]() ,
,![]() 与
与![]() 都关于
都关于![]() 轴对称,且
轴对称,且![]() 的方程为
的方程为![]() ,由此易知
,由此易知![]() 与
与![]() 的公共点的坐标为
的公共点的坐标为![]() ,∴
,∴![]() ②,联立①,②,得
②,联立①,②,得![]() ,
,![]() ,故
,故![]() 的方程为
的方程为![]() ;(2)如图
;(2)如图![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(i)∵![]() 与
与![]() 同向,且
同向,且![]() ,∴
,∴![]()
![]() ,从而
,从而![]()
![]() ,即
,即![]()
![]() ,于是
,于是![]()
![]()
![]()
![]() ③,设直线
③,设直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,由
,由![]() 得
得![]() ,而
,而![]() ,
,![]() 是这个方程的两根,∴
是这个方程的两根,∴![]() ,
,![]() ④,由
④,由 得
得![]() ,而
,而![]() ,
,![]() 是这个方程的两根,∴
是这个方程的两根,∴![]()
![]() ,
,![]()
![]() ⑤,将④⑤带入③,得
⑤,将④⑤带入③,得![]() ,即
,即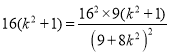 ,
,
∴![]()
![]() ,解得
,解得![]() ,即直线
,即直线![]() 的斜率为
的斜率为![]() .
.
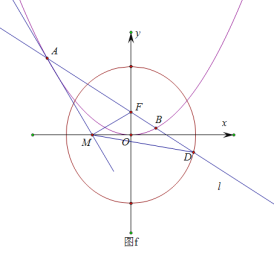
(ii)由![]() 得
得![]()
![]() ,∴
,∴![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即
![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,∴
,∴![]() ,而
,而![]() ,于是
,于是
![]()
![]()
![]() ,因此
,因此![]() 是锐角,从而
是锐角,从而![]() 是钝角.,故直线
是钝角.,故直线![]() 绕点
绕点![]() 旋转时,
旋转时,![]() 总是钝角三角形.
总是钝角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目