题目内容
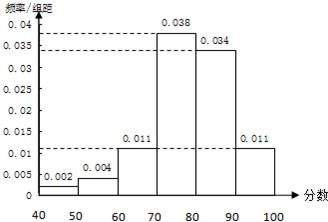 22、某校高二年级的一次数学统考中,随机抽取100名同学的成绩,数据按如下方式分组:(40,50],(50,60],(60,70],(70,80],(80,90],(90,100],得到频率分布直方图如下:
22、某校高二年级的一次数学统考中,随机抽取100名同学的成绩,数据按如下方式分组:(40,50],(50,60],(60,70],(70,80],(80,90],(90,100],得到频率分布直方图如下:(1)若该校高二学生有1000人,试估计这次统考该校高二学生的分数在区间(60,90]内的人数;
(2)根据样本的频率分布直方图,估计该校高二年级学生这次数学统考成绩的平均数和中位数(精确到0.01)
分析:(1)根据直方图中的各个矩形的面积代表了频率,求出成绩大于等于60分且小于90分的学生的频率,然后根据“频数=频率×样本容量”求出所求即可.
(2)根据平均数和中位数结合样本的频率分布直方图,求得样本中该校高二年级学生这次数学统考成绩的平均数和中位数
,再根据平均数和中位数的概念,用样本的频率分布估计总体分布进行分析即可.
(2)根据平均数和中位数结合样本的频率分布直方图,求得样本中该校高二年级学生这次数学统考成绩的平均数和中位数
,再根据平均数和中位数的概念,用样本的频率分布估计总体分布进行分析即可.
解答:解:(1)由频率分布直方图得,
分数在区间(60,90]的频率为0.83,
则高二学生的分数在区间(60,90]内的人数为1000×0.83=830.(3分)
(2)根据样本的频率分布直方图,
可估算样本平均数为45×0.02+55×0.04+65×0.11+75×0.38+85×0.34+95×0.11=78.1
在频率分步直方图中,小正方形的面积表示这组数据的频率,
中位数是所有数中最中间一个或中间两个的平均数
把每一部分的小正方形的面积做出来,
得到78.68左右两边的矩形面积和各为0.5.
可估算样本中位数为:78.68.
分数在区间(60,90]的频率为0.83,
则高二学生的分数在区间(60,90]内的人数为1000×0.83=830.(3分)
(2)根据样本的频率分布直方图,
可估算样本平均数为45×0.02+55×0.04+65×0.11+75×0.38+85×0.34+95×0.11=78.1
在频率分步直方图中,小正方形的面积表示这组数据的频率,
中位数是所有数中最中间一个或中间两个的平均数
把每一部分的小正方形的面积做出来,
得到78.68左右两边的矩形面积和各为0.5.
可估算样本中位数为:78.68.
点评:本题考查频率分布直方图的相关知识,直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1,频数=频率×样本容量,属于基础题.

练习册系列答案
相关题目
(本题满分12分)
对某校高二年级学生参加社会实践活动次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践活动的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
26 |
n |
|
|
m |
P |
|
|
1 |
0.025 |
|
合计 |
M |
1 |

(Ⅰ)求出表中M,P及图中 的值;
的值;
(Ⅱ)在所取样本中,从参加社会实践活动的次数不少于20次的学生中任选2人,求恰有一人参加社会实践活动次数在区间 内的概率.
内的概率.
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
| [3,6) | 10 | m |
| [6,9) | n | p |
| [9,12) | 4 | q |
| [12,15] | 2 | 0.05 |
| 合计 | N | 1 |
(1)求出表中N,p及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于9次的学生中任选2人,求至少有一人参加社区服务次数在区间[12,15]内的概率.

对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
(1)求出表中N,p及图中a的值;
(2)在所取样本中,从参加社区服务的次数不少于9次的学生中任选2人,求至少有一人参加社区服务次数在区间[12,15]内的概率.

| 分组 | 频数 | 频率 |
| [3,6) | 10 | m |
| [6,9) | n | p |
| [9,12) | 4 | q |
| [12,15] | 2 | 0.05 |
| 合计 | N | 1 |
(2)在所取样本中,从参加社区服务的次数不少于9次的学生中任选2人,求至少有一人参加社区服务次数在区间[12,15]内的概率.

 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: 对某校高二年级学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图(如图):
对某校高二年级学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图(如图):

