题目内容
设函数g(x)=x2-2(x∈R), 若函数y=f(x)图象与直线y=k(k为常数)有且只有一个交点,则k的取值范围是
若函数y=f(x)图象与直线y=k(k为常数)有且只有一个交点,则k的取值范围是
- A.[-
 ,0]∪(8,+∞)
,0]∪(8,+∞) - B.{-
 }∪(2,8)
}∪(2,8) - C.(2,+∞)
- D.[-
 ,0]∪(2,+∞)
,0]∪(2,+∞)
B
分析:先将原函数化成f(x)=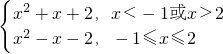 ,画出其图象,如图所示.数形结合可得k的取值范围.
,画出其图象,如图所示.数形结合可得k的取值范围.
解答: 解:函数
解:函数
=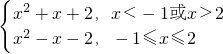 ,
,
如图所示:若直线y=k与y=f(x)的图象只有一个交点,则有 k∈{- }∪(2,8),
}∪(2,8),
故选B.
点评:本题主要考查二次函数、分段函数的性质,体现了数形结合的数学思想,属于基础题.
分析:先将原函数化成f(x)=
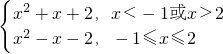 ,画出其图象,如图所示.数形结合可得k的取值范围.
,画出其图象,如图所示.数形结合可得k的取值范围.解答:
 解:函数
解:函数
=
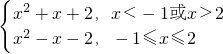 ,
,如图所示:若直线y=k与y=f(x)的图象只有一个交点,则有 k∈{-
 }∪(2,8),
}∪(2,8),故选B.
点评:本题主要考查二次函数、分段函数的性质,体现了数形结合的数学思想,属于基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目