题目内容
当x∈(0,+∞)时,幂函数y=(m2-m-1)x-5m-3为减函数,求实数m的值。
解:因 当x∈(0,+∞)时,幂函数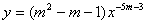 为减函数,
为减函数,
所以,m2-m-1=0,且-5m-3<0,
即m=2或m=-1,且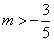 ,
,
所以,m=2。
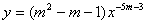 为减函数,
为减函数,所以,m2-m-1=0,且-5m-3<0,
即m=2或m=-1,且
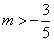 ,
,所以,m=2。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义域R的函数f(x)满足f(x+2)=3f(x),当x∈[0,2]时,f(x)=x2-2x,若x∈[-4,-2]时,f(x)≥
(
-t)恒成立,则实数t的取值范围是( )
| 1 |
| 18 |
| 3 |
| t |
| A、(-∞,-1]∪(0,3] | ||||
B、(-∞,-
| ||||
| C、[-1,0)∪[3,+∞) | ||||
D、[-
|
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<