题目内容
直线![]() 过抛物线
过抛物线![]() 的焦点,并且与抛物线相交于
的焦点,并且与抛物线相交于![]() 和
和![]() 两点
两点![]() .求证:对于此抛物线的任意给定的一条弦
.求证:对于此抛物线的任意给定的一条弦![]() ,直线
,直线![]() 不是
不是![]() 的垂直平分线.用反证法证明.
的垂直平分线.用反证法证明.
证明见解析
解析:
证明:假设直线![]() 是
是![]() 的垂直平分线,设
的垂直平分线,设![]() 的斜率为
的斜率为![]() ,则
,则![]() 的方程是
的方程是![]() .
.
设直线![]() 与
与![]() 轴的交点坐标为
轴的交点坐标为![]() ,则
,则![]() 的方程是
的方程是![]() .
.
设![]() 的坐标分别为
的坐标分别为![]() ,则
,则![]() 的中点坐标是
的中点坐标是![]() .
.
可知![]() ,
,![]() 是方程组
是方程组 的两组解.
的两组解.
方程组消去![]() ,得
,得![]() . ①
. ①
显然,![]() ,方程①有两个不等的实数根,故
,方程①有两个不等的实数根,故![]() ,
,
于是有![]() ,
,![]() .
.
但![]() 的中点坐标满足方程
的中点坐标满足方程![]() ,
,
![]() ,
,
即![]() ,
,
![]() .
.
因此有![]() ,
,
这与①式中![]() 矛盾,原假定不成立.
矛盾,原假定不成立.
所以,直线![]() 不是
不是![]() 的垂直平分线.
的垂直平分线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(本小题满分14分)设椭圆 与抛物线
与抛物线 的焦点均在
的焦点均在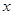 轴上,
轴上, 的中心和
的中心和 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)求 ,
, 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率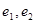 ;
;
2)设直线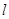 与椭圆
与椭圆 交于不同的两点
交于不同的两点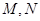 ,且
,且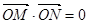 (其中
(其中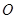 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线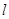 过抛物线
过抛物线 的焦点
的焦点 若存在,求出直线
若存在,求出直线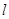 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
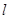 过抛物线
过抛物线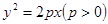 的焦点,且交抛物线于
的焦点,且交抛物线于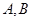 两点,交其准线于
两点,交其准线于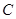 点,已知
点,已知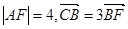 ,则
,则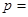
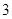
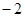
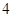

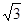
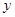
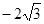

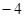
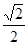
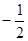
 过抛物线
过抛物线 的焦点F,且和
的焦点F,且和 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
 B.
B. C.
C.
 D.
D. 