题目内容
直线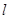 过抛物线
过抛物线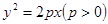 的焦点,且交抛物线于
的焦点,且交抛物线于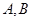 两点,交其准线于
两点,交其准线于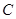 点,已知
点,已知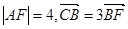 ,则
,则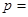
【答案】

【解析】
试题分析:作 垂直准线于D,作BE垂直准线于E,
垂直准线于D,作BE垂直准线于E,
 ,设准线交x轴于G,
,设准线交x轴于G, 
考点:直线与抛物线相交弦长问题
点评:本题中充分利用抛物线定义:抛物线上的点到焦点的距离等于到准线的距离,使计算得到了简化

练习册系列答案
相关题目
(本小题满分14分)设椭圆 与抛物线
与抛物线 的焦点均在
的焦点均在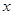 轴上,
轴上, 的中心和
的中心和 的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
的顶点均为原点,从每条曲线上至少取两个点,将其坐标记录于下表中:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)求 ,
, 的标准方程, 并分别求出它们的离心率
的标准方程, 并分别求出它们的离心率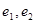 ;
;
2)设直线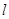 与椭圆
与椭圆 交于不同的两点
交于不同的两点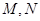 ,且
,且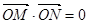 (其中
(其中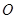 坐标原点),请问是否存在这样的直线
坐标原点),请问是否存在这样的直线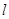 过抛物线
过抛物线 的焦点
的焦点 若存在,求出直线
若存在,求出直线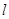 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
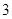
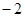


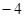
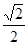
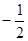
 过抛物线
过抛物线 的焦点F,且和
的焦点F,且和 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
 B.
B. C.
C.
 D.
D. 