题目内容
在平面直角坐标系中，点集
，
，
则（1）点集
所表示的区域的面积为_____；
（2）点集
所表示的区域的面积为 .
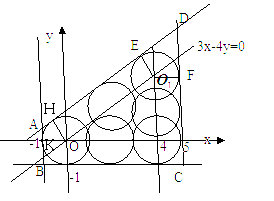
（1）
（2）
解析:
（1）集合A表示的区域为以原点为圆心，1为半径包括边界的圆面，集合B表示以x轴正半轴和直线
，及
为边的三角形区域（包括边界）。点P所表示的区域为以
为圆心，1为半径包括边界的圆面，所以圆的面积为
。（2）点
表示的区域为
集合
所表示的区域为梯形
所围成的区域，去掉圆与梯形四个角围成的图形。易知直线
方程为
，
方程
，
点坐标为
点坐标为3x-4y=0与
的交点为
，
点坐标为直线
与直线
的交点，直线
与直线的距离为1，由两平行线的距离可得直线方程为
，所以A点坐标为
，由勾股定理知
，同理得AH=
=
，
=6，
圆与梯形相切的下面两个角的面积和为（
）
2=2
，因为圆与梯形相切的上面两个角的面积为
两圆半径都为1，所以两段圆弧的面积
扇形
扇形
=
=
=
，所以集合Q所围成的面积为
=
另解：集合Q所围成的面积为三个矩形面积加上一个大三角形面积加上四段扇形的面积，而这四段扇形的面积恰好为一个圆的面积。故S=
=18+
练习册系列答案
相关题目