题目内容
1.函数f(x)=x•2|x|-x-1的零点个数为( )| A. | 2 | B. | 3 | C. | 0 | D. | 1 |
分析 注意到绝对值,分x<0与x≥0讨论,从而函数的单调性及函数零点的判定定理判断零点的个数.
解答 解:当x<0时,
f(x)=x•2|x|-x-1=x(2|x|-1)-1<-1;
故函数f(x)=x•2|x|-x-1在(-∞,0)上没有零点;
当x≥0时,
f(x)=x•2x-x-1
f′(x)=2x+xln2•2x-1
=xln2•2x+2x-1≥0;
故f(x)=x•2x-x-1在[0,+∞)上是增函数,
且f(0)=-1,f(2)=8-2-1=5>0;
故函数f(x)=x•2|x|-x-1在[0,+∞)上有且只有一个零点;
综上所述,函数f(x)=x•2|x|-x-1的零点个数为1;
故选:D.
点评 本题考查了函数的单调性的判断及函数零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=-2x-1+$\frac{1}{{{2^{x+1}}}}$,g(x)=x3-3x,那么函数y=f(g(x))是( )
| A. | 奇函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| B. | 奇函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 | |
| C. | 偶函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| D. | 偶函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 |
16.已知函数f(x)=x2-cosx,若当-π<x<π时,f(x1)<f(x2)恒成立,则下列结论一定成立的是( )
| A. | x1>x2 | B. | x1<x2 | C. | x12<x22 | D. | |x1|>|x2| |
 的离心率为
的离心率为 ,以
,以 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线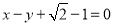 相切.
相切. 的标准方程;
的标准方程; ,和面内一点
,和面内一点 ,过点
,过点 任作直线
任作直线 与椭圆
与椭圆 相交于
相交于 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 ,若
,若 ,试求
,试求 满足的关系式.
满足的关系式. 及直线
及直线 所围成的封闭图形为区域
所围成的封闭图形为区域 ,不等式组
,不等式组 所确定的区域为
所确定的区域为 ,在区域
,在区域 内随机取一点,该点恰好在区域
内随机取一点,该点恰好在区域 的概率为( )
的概率为( ) B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.