题目内容
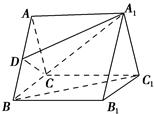
如图,在四棱锥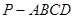 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,
, ,
, 为
为 中点.
中点.
(1)证明: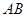 //平面
//平面 ;
;
(2)证明: 平面
平面 .
.
(1)参考解析;(2)参考解析
解析试题分析:(1)直线与平面平行的证明,根据判断定理要在平面内找一条直线与与该直线平行.所以要证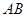 //平面
//平面 ,找到直线
,找到直线 即可.
即可.
(2)要证直线与平面垂直根据判断定理要在平面内找到两条相交的直线与该直线垂直即可.通过分析直线AE⊥PD由题意可得;另外直线CD垂直平面PAD,所以有可得直线CD垂直直线AE.又由于直线CD与直线PD相交,所以可证得结论.
试题解析:证明:(1)因为底面 为矩形,
为矩形,
所以  .又因为
.又因为  平面
平面 ,
, 平面
平面 ,
,
所以 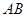 //平面
//平面 .
.
(2)因为 ,
, 为
为 中点,
中点,
所以 ,因为
,因为  平面
平面 ,
,
所以

 .又底面
.又底面 为矩形,
为矩形,
所以 .
.
所以 平面
平面 .
.
所以
 .
.
所以 平面
平面 .
.
考点:1.线面平行的判断.2.线面垂直的判断.3.线面关系与线线关系的相互转化.4.空间图像感.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目

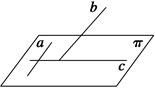
 的底面
的底面 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 分别为
分别为 的中点.
的中点.
 ;(2)
;(2) ∥平面
∥平面 .
.
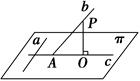
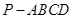 中,底面
中,底面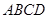 是平行四边形,
是平行四边形,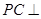 平面
平面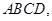
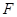 是
是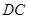 的中点,
的中点,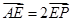 .
.
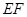 与平面
与平面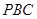 的位置关系,并予以证明;
的位置关系,并予以证明;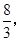
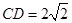 ,
,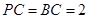 ,求证:平面
,求证:平面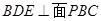 .
.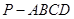 中,底面
中,底面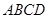 为直角梯形,
为直角梯形,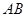 ∥
∥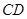 ,
, 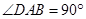 ,
,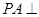 平面
平面 ,且
,且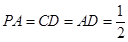 ,
,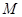 为
为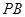 的中点
的中点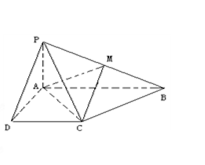
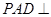 面
面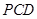
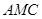 与面
与面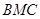 夹角的余弦值.
夹角的余弦值. 是边长为2的正三角形,若
是边长为2的正三角形,若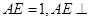 平面
平面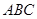 ,平面
,平面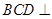 平面
平面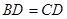 ,且
,且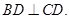
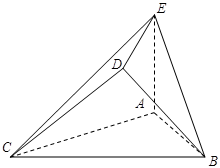
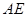 //平面
//平面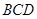 ;
;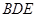
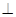 平面
平面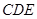 。
。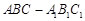 中,
中,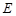 ,
,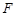 分别为
分别为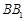 ,
,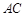 的中点.
的中点.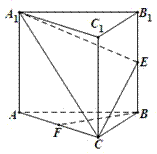
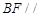 平面
平面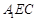 ;
;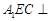 平面
平面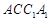 .
.