题目内容
5．画出下列函数的图象，并根据图象指出函数的单调区间和值域．（1）f（x）=$\left\{\begin{array}{l}{x，-1＜x＜1}\\{-x，x＜-1或x＞1}\end{array}\right.$；
（2）g（x）=（x+1）•|x|
分析 描点画图，根据图象可得到结论．
解答 解：（1）f（x）=$\left\{\begin{array}{l}{x，-1＜x＜1}\\{-x，x＜-1或x＞1}\end{array}\right.$的图象如图所示，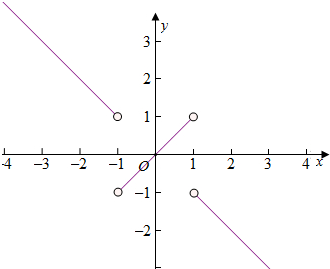
由图象可知，f（x）在（-1，1）为增函数，在（-∞，-1）和（1，+∞）为减函数，
其值域为（-∞，-1）∪（-1，1）∪（1，+∞）；
（2）g（x）=（x+1）•|x|=$\left\{\begin{array}{l}{{x}^{2}+x，x≥0}\\{-{x}^{2}-x，x＜0}\end{array}\right.$，图象为，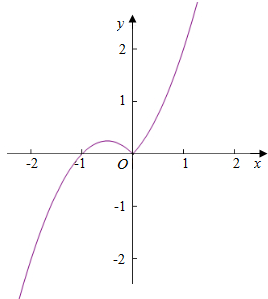
由图象可知，f（x）在（-∞，-$\frac{1}{2}$），（0，+∞）为增函数，在（-$\frac{1}{2}$，0）为减函数，
其值域为R．
点评 本题考查了分段函数的图象的画法和识别，属于基础题．
练习册系列答案
相关题目
14．定义在[-1，1]上的偶函数y=f（x）满足：对于任意的x1，x2∈[0，1]（x1≠x2），都有（x2-x1）（f（x2）-f（x1））＞0，则满足f（2x-1）≤f（2x）的x的取值范围是（ ）
| A． | [$\frac{1}{4}$，$\frac{1}{2}$] | B． | [$\frac{1}{4}$，1] | C． | [0，1] | D． | [0，$\frac{1}{2}$] |