题目内容
定义在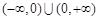 上的函数
上的函数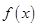 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,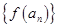 仍是等比数列,则称
仍是等比数列,则称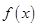 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在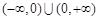 上的如下函数:
上的如下函数:
①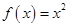 ②
②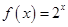 ③
③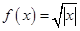 ④
④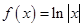
则其中是“保等比数列函数”的 的序号为( )
的序号为( )
| A.①② | B.③④ | C.①③ | D.②④ |
C
解析试题分析:等比数列性质, ,①
,① ; ②
; ② ;③
;③ ;④
;④ .选C
.选C
考点:本题考查了等比数列的性质
点评:对于新定义型问题,熟练运用题目定义是解决问题的关键,属基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在各项为正的等比数列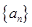 中,
中, ,前三项和为21,则
,前三项和为21,则 等于( )
等于( )
| A.189 | B.84 | C.72 | D.33 |
等比数列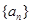 中,
中,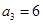 ,前三项和
,前三项和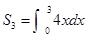 ,则公比
,则公比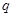 的值为
的值为
A.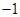 或 或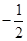 | B.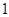 或 或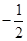 | C.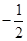 | D.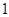 |
设等比数列 的前项和为
的前项和为 ,若
,若 ,则
,则
| A.2 | B. | C. | D.3 |
数列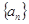 满足
满足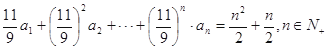 ,当
,当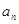 取最大值时,n= ( )
取最大值时,n= ( )
A.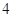 | B. | C.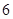 | D.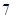 |
公比为2的等比数列{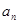 }的各项都是正数,且
}的各项都是正数,且
 =16,则
=16,则
A. | B. | C. | D. |
设等比数列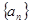 的公比为q,前n项和为
的公比为q,前n项和为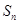 ,若
,若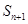 ,
,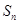 ,
,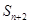 成等差数列,则公比q为( )
成等差数列,则公比q为( )
A.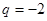 | B.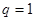 | C.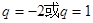 | D.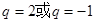 |
若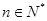 ,则1+2+22+23+…+2n-1=
,则1+2+22+23+…+2n-1=
| A.2n-1-1 | B.2n-1 | C.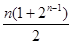 | D.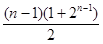 |
已知等比数列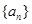 的公比为正数,且
的公比为正数,且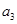
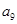 =2
=2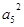 ,
,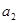 =1,则
=1,则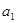 =( )
=( )
A.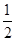 | B.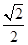 | C.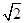 | D.2 |