题目内容
(本题满12分)在 中,角
中,角 的对边分别为
的对边分别为 且
且
(1)求 的值;
的值;
(2)若 ,且
,且 ,求
,求 的值.
的值.
(1)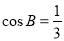 ;(2)
;(2)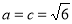 .
.
【解析】
试题分析:(1)熟悉三角公式的整体结构,灵活变换,要熟悉三角公式的代数结构,更要掌握公式中角和函数名称的特征,要体会公式间的联系,掌握常见的公式变形;(2)在三角形中处理边角关系时,一般全部转化为角的关系,或全部转化为边的关系.题中若出现边的一次式一般采用正弦定理,出现边的二次式一般采用余弦定理,应用正弦、余弦定理时,注意公式变形的应用,解决三角形问题时,注意角的限制范围,在三角形中,注意隐含条件 (3)解决三角形问题时,根据边角关系灵活的选用定理和公式.
(3)解决三角形问题时,根据边角关系灵活的选用定理和公式.
试题解析:(1)由正弦定理得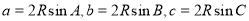 ,
,
则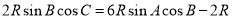
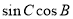
故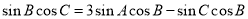
可得
即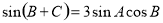
因此得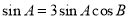 ,
,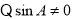 ,得
,得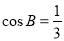
【解析】
由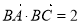 ,可得
,可得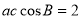 ,
,
又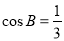 ,故
,故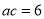 ,由
,由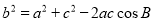 ,得
,得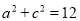 ,
,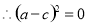
所以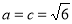 .
.
考点:正余弦定理的应用.
考点分析: 考点1:三角形的解的情况 考点2:解三角形 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 是
是 的高,
的高, 是
是 外接圆的直径,若
外接圆的直径,若 ,则
,则 .
.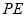 切⊙
切⊙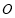 于点
于点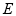 ,割线
,割线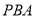 交⊙
交⊙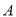 、
、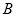 两点,
两点,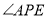 的平分线和
的平分线和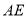 、
、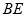 分别交于点
分别交于点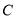 、
、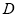 .求证:
.求证: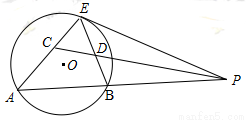
 ;
; 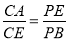 .
. 的前
的前 项和为
项和为 ,若
,若 ,则
,则
 B.
B. C.
C. D.
D.
 为圆
为圆 的切线,
的切线, 为切点,
为切点,
 ,
,
 的角平分线与
的角平分线与 和圆
和圆 和
和 .
.

 的值.
的值.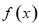 是定义在
是定义在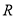 上的恒不为零的函数,对任意实数
上的恒不为零的函数,对任意实数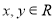 ,都有
,都有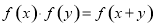 ,若
,若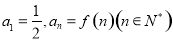 ,则数列
,则数列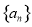 的前
的前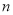 项和
项和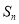 的取值范围是( )
的取值范围是( )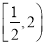 B.
B. 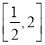 C.
C. 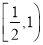 D.
D. 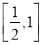
 的夹角为
的夹角为 ,
, ( )
( ) B.
B. C.
C. D.
D.
 满足
满足 其中
其中 是自然对数的底数,则
是自然对数的底数,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.
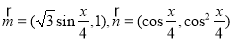 ,记
,记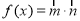
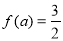 ,求
,求 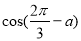 的值;
的值;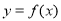 的图象向右平移
的图象向右平移 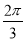 个单位得到
个单位得到 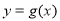 的图象,若函数
的图象,若函数 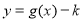 在
在 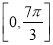 上有零点,求实数k的取值范围.
上有零点,求实数k的取值范围.