题目内容
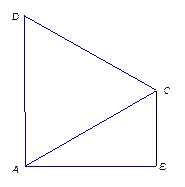
如图1,在直角梯形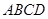 中,
中,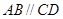 ,
, ,且
,且 .
.
现以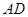 为一边向形外作正方形
为一边向形外作正方形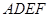 ,然后沿边
,然后沿边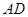 将正方形
将正方形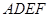 翻折,使平面
翻折,使平面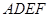 与平面
与平面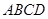 垂直,
垂直, 为
为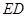 的中点,如图2.
的中点,如图2.
(1)求证: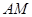 ∥平面
∥平面 ;
;
(2)求证: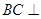 平面
平面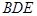 ;
;
(3)求点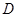 到平面
到平面 的距离.
的距离.
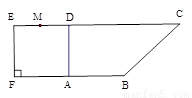

图 图
图
(1)利用线线平行证明线面平行;(2)利用线线垂直证明线面垂直;(3)利用等体积法求解点到面平面的距离
【解析】
试题分析:
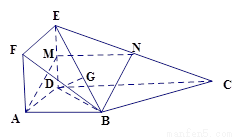
解:(1)证明:取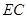 中点
中点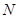 ,连结
,连结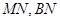 .
.
在△ 中,
中,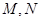 分别为
分别为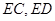 的中点, 所以
的中点, 所以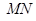 ∥
∥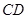 ,且
,且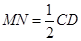 .
.
由已知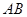 ∥
∥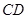 ,
,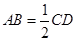 , 所以
, 所以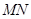 ∥
∥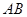 ,且
,且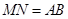 .
3分
.
3分
所以四边形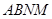 为平行四边形. 所以
为平行四边形. 所以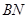 ∥
∥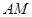 .
4分
.
4分
又因为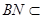 平面
平面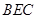 ,且
,且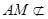 平面
平面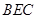 ,所以
,所以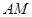 ∥平面
∥平面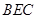 .
5分
.
5分
(2)证明:在正方形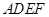 中,
中,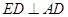 .
.
又因为平面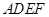
 平面
平面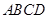 ,且平面
,且平面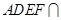 平面
平面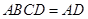 ,
,
所以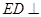 平面
平面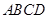 . 所以
. 所以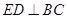 .
7分
.
7分
在直角梯形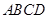 中,
中,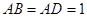 ,
,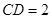 ,可得
,可得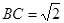 .
.
在△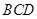 中,
中, ,
,
所以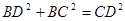 .所以
.所以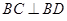 . 8分
. 8分
所以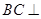 平面
平面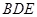 .
10分
.
10分
(3)解法一:由(2)知,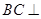 平面
平面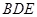
又因为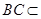 平面
平面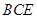 , 所以平面
, 所以平面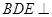 平面
平面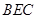 .
11分
.
11分
过点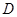 作
作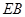 的垂线交
的垂线交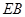 于点
于点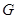 ,则
,则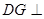 平面
平面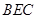
所以点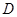 到平面
到平面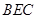 的距离等于线段
的距离等于线段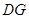 的长度
12分
的长度
12分
在直角三角形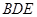 中,
中,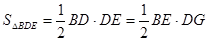
所以
所以点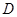 到平面
到平面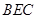 的距离等于
的距离等于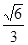 . 14分
. 14分
解法二:由(2)知,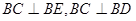
所以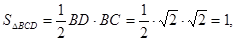
 12分
12分
又 ,设点
,设点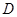 到平面
到平面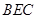 的距离为
的距离为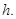
则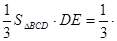
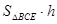 , 所以
, 所以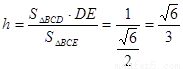
所以点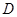 到平面
到平面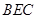 的距离等于
的距离等于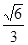 . 14分
. 14分
考点:本题考查了空间中的线面关系
点评:立体几何问题主要是探求和证明空间几何体中的平行和垂直关系以及空间角、体积等计算问题.对于平行和垂直问题的证明或探求,其关键是把线线、线面、面面之间的关系进行灵活的转化.在寻找解题思路时,不妨采用分析法,从要求证的结论逐步逆推到已知条件.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 中,
中,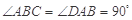 ,
,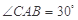 ,
,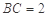 ,
,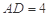 . 把
. 把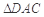 沿对角线
沿对角线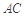 折起到
折起到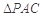 的位置,如图2所示,使得点
的位置,如图2所示,使得点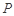 在平面
在平面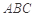 上的正投影
上的正投影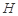 恰好落在线段
恰好落在线段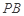 ,点
,点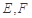 分别为线段
分别为线段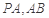 的中点.
的中点. 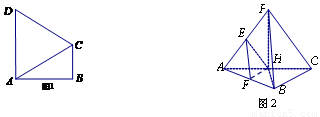
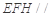 平面
平面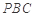 ;
;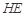 与平面
与平面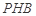 所成角的正弦值;
所成角的正弦值;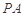 上是否存在一点
上是否存在一点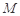 ,使得
,使得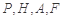 四点的距离相等?请说明理由.
四点的距离相等?请说明理由. 中,
中, ,
, ,
,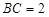 ,
,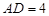 . 把
. 把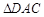 沿对角线
沿对角线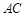 折起到
折起到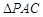 的位置,如图2所示,使得点
的位置,如图2所示,使得点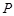 在平面
在平面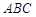 上的正投影
上的正投影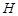 恰好落在线段
恰好落在线段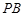 ,点
,点 分别为线段
分别为线段 的中点.
的中点. 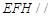 平面
平面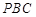 ;
;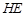 与平面
与平面 所成角的正弦值;
所成角的正弦值;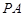 上是否存在一点
上是否存在一点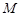 ,使得
,使得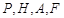 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.
 中,
中,  ,
,  ,
, ,
, 为线段
为线段 的中点. 将
的中点. 将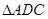 沿
沿 折起,使平面
折起,使平面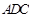
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示. 平面
平面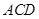 ;
;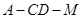 的余弦值.
的余弦值. 
 中,
中,  ,
,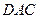 沿对角线
沿对角线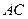 折起后如图2所示(点
折起后如图2所示(点 记为点
记为点 ), 点
), 点 上的正投影
上的正投影 落在线段
落在线段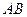 上, 连接
上, 连接 .
. 与平面
与平面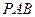 所成的角的大小;
所成的角的大小; 的大小的余弦值.
的大小的余弦值.