Question

已知f(x)=2^x-1,g(x)=1-x²，规定:当|f(x)|≥g(x)时,h(x)=|f(x)|;当|f(x)|＜g(x)时,h(x)=-g(x).试讨论h(x)是否有最大值或最小值,并说明理由.

Answer 1

解：画出y=|f(x)|=|2^x-1|与y=g(x)=1-x²的图象,它们交于A、B两点.由“规定”，在A、B两侧,|f(x)|≥g(x),故h(x)=|f(x)|;在A、B之间,|f(x)|＜g(x),故h(x)=-g(x).

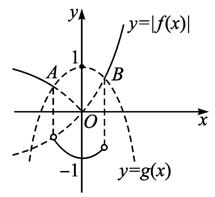
    综上可知,y=h(x)的图象是图中的实线部分,因此h(x)有最小值-1,无最大值.