题目内容
设函数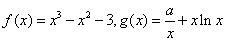 ,其中
,其中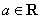 .
.
(1)若存在 ,使得
,使得 ,求整数
,求整数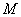 的最大值;
的最大值;
(2)若对任意的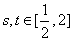 ,都有
,都有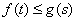 ,求
,求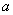 的取值范围.
的取值范围.
解:(1) ,令
,令 得
得 ,
,
当 变化时,
变化时, 和
和 的变化情况如下:
的变化情况如下:
|
| 0 |
|
|
| 2 |
|
| - | 0 | + | ||
|
|
| 单调递减 | 极小值 | 单调递增 | 1 |
可得, ,
, .
.
要使存在 ,使得
,使得 ,只需
,只需
 ,故整数
,故整数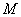 的最大值为
的最大值为 .
.
(2)由(1)知,在 上,
上, ,要满足对任意的
,要满足对任意的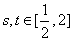 ,都有
,都有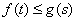 ,只需
,只需 在
在 上恒成立,
上恒成立,
即 在
在 上恒成立,分离参数可得:
上恒成立,分离参数可得: ,
,
令 ,可知,当
,可知,当 单调递增,当
单调递增,当 单调递减,
单调递减,
所以 在
在 处取得最大值
处取得最大值 ,
,
所以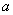 的取值范围是
的取值范围是 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij,则数字73在表中出现的次数为 _________ .
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 3 | 5 | 7 | 9 | 11 | 13 | … |
| 4 | 7 | 10 | 13 | 16 | 19 | … |
| 5 | 9 | 13 | 17 | 21 | 25 | … |
| 6 | 11 | 16 | 21 | 26 | 31 | … |
| 7 | 13 | 19 | 25 | 31 | 37 | … |
| … | … | … | … | … | … | … |




 与曲线
与曲线 围成图形的面积为
围成图形的面积为  成等比数列,非零实数
成等比数列,非零实数 分别为
分别为 ,
, 的等差中项,则下列结论正确的是
的等差中项,则下列结论正确的是  B.
B. C.
C. D.
D.
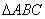 是边长为3的正三角形,若在每一边的两个三等分点中,各随机选取一点连成三角形,下列命题正确的是(写出所有正确命题的编号):
是边长为3的正三角形,若在每一边的两个三等分点中,各随机选取一点连成三角形,下列命题正确的是(写出所有正确命题的编号): 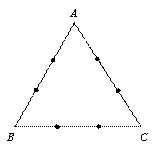
 的展开式中x3的系数为 _________ .
的展开式中x3的系数为 _________ . 中,
中, 则该数列的前
则该数列的前 项和
项和 ( )
( ) C.
C. D.
D.