题目内容
设函数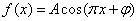 (其中
(其中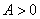 ,
, ,
, ).当
).当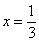 时,
时,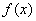 取得最小值
取得最小值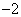 .
.
(1)求函数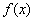 的解析式;
的解析式;
(2)求函数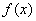 的单调递增区间.
的单调递增区间.
解:(1)由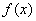 最小值
最小值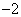 ,且
,且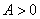 ,所以
,所以 .………………………2分
.………………………2分
因为 ,所以
,所以 , ………………………………………4分
, ………………………………………4分
由 可得
可得 ,所以
,所以 ,所以
,所以 . …………6分
. …………6分
故 的解析式为
的解析式为 . ………………………7分
. ………………………7分
(2)
由 ,
, , …………………………9分
, …………………………9分
解得 ,
, , ………………………11分
, ………………………11分
∴函数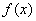 的单调递增区间为
的单调递增区间为 .……………12分
.……………12分

练习册系列答案
相关题目
下表是抽测某校初二女生身高情况所得的部分资料(身高单位:cm,测量时精确到1cm).已知身高在151cm 以下(含151cm)的被测女生共3人.则所有被测女生总数为 .
| 分组 | [145.5,148.5) | [148.5,151.5) | [151.5,154.5) | [154.5,157.5) | [157.5,160.5) | [160.5,163.5) | [163.5,166.5) | [166.5,169.5] |
| 频率 | 0.02 | 0.04 | 0.08 | 0.12 | 0.30 | 0.20 | 0.18 | 0.06 |
 上一点
上一点 到焦点的距离为
到焦点的距离为 ,则点
,则点 轴的距离是 .
轴的距离是 . ,该函数在区间
,该函数在区间 上的最大值是 .
上的最大值是 . ,那么
,那么 等于( )
等于( ) B.
B.
 D.
D.
 的三个顶点的直角坐标分别为
的三个顶点的直角坐标分别为 ,且
,且  为
为 的取值范围为____________.
的取值范围为____________.
 中,
中, ,点P在边
,点P在边 上,则
上,则 的最大值为 .
的最大值为 . 的不等式
的不等式 ,
,
 ,求a的值;
,求a的值;