题目内容
已知“|x-1|≤1”是“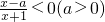
”的充分不必要条件，则实数a的取值范围是________．
（2，+∞）
分析：求出|x-1|≤1的解，利用已知条件，转化分式不等式为二次不等式，求出a的范围即可．
解答：|x-1|≤1的解为0≤x≤2，
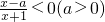化为（x+1）（x-a）＜0，即-1＜x＜a．
因为“|x-1|≤1”是“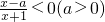”的充分不必要条件，
所以a＞2．
所以实数a的取值范围是（2，+∞）．
故答案为：（2，+∞）．
点评：本题考查必要条件、充分条件与充要条件的判断，不等式的解法，考查转化思想计算能力．
分析：求出|x-1|≤1的解，利用已知条件，转化分式不等式为二次不等式，求出a的范围即可．
解答：|x-1|≤1的解为0≤x≤2，
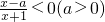化为（x+1）（x-a）＜0，即-1＜x＜a．因为“|x-1|≤1”是“
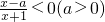”的充分不必要条件，所以a＞2．
所以实数a的取值范围是（2，+∞）．
故答案为：（2，+∞）．
点评：本题考查必要条件、充分条件与充要条件的判断，不等式的解法，考查转化思想计算能力．
练习册系列答案
同步练习强化拓展系列答案
相关题目