题目内容
 如图,在三棱锥C-OAB中,OA⊥OB,CB⊥平面OAB,OA=2,OB=4,BC=6,M为AC的中点,求:
如图,在三棱锥C-OAB中,OA⊥OB,CB⊥平面OAB,OA=2,OB=4,BC=6,M为AC的中点,求:
(1)直线OM与AB所成角的余弦值;
(2)直线AB与平面OAC所成角的正弦值.
解:(1)建立如图所示的坐标系,有O(0,0,0),A(2,0,0),
B(0,4,0),C(0,4,6),M(1,2,3)
∴ ,
,
∴ =-2+8+0=6
=-2+8+0=6
∴cos< >=
>= =
=
(2)设平面OAC的法向量为 ,
,
则 ,
,
∴2a=0,
4b+6c=0,
∴
设直线AB与平面OAC所成的角是θ,
∴sinθ=|cos< >=
>=
分析:(1)根据所给的图形,建立坐标系,写出点的坐标,得到对应的向量,根据两个向量的夹角的余弦,写出两条异面直线的余弦值.
(2)设出平面的法向量,根据法向量与平面上两条不共线的向量的数量积等于0,得到平面的一个法向量,根据两个向量之间夹角的余弦值等于线面之间的夹角的正弦值.
点评:本题考查直线与平面所成的角和线面角,本题解题的关键是建立坐标系,把繁琐的理论证明变换成了数字的运算.
B(0,4,0),C(0,4,6),M(1,2,3)
∴
 ,
,
∴
 =-2+8+0=6
=-2+8+0=6∴cos<
 >=
>= =
=
(2)设平面OAC的法向量为
 ,
,则
 ,
,
∴2a=0,
4b+6c=0,
∴

设直线AB与平面OAC所成的角是θ,
∴sinθ=|cos<
 >=
>=
分析:(1)根据所给的图形,建立坐标系,写出点的坐标,得到对应的向量,根据两个向量的夹角的余弦,写出两条异面直线的余弦值.
(2)设出平面的法向量,根据法向量与平面上两条不共线的向量的数量积等于0,得到平面的一个法向量,根据两个向量之间夹角的余弦值等于线面之间的夹角的正弦值.
点评:本题考查直线与平面所成的角和线面角,本题解题的关键是建立坐标系,把繁琐的理论证明变换成了数字的运算.

练习册系列答案
相关题目
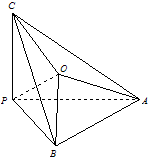 如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPA=45°,∠OPB=60°,则∠OPC的度数为( )
如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPA=45°,∠OPB=60°,则∠OPC的度数为( )| A、30° | B、45° | C、60° | D、75° |
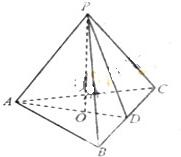 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上.
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上. 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.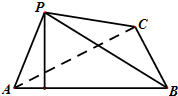 (2012•四川)如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,点P在平面ABC内的射影O在AB上.
(2012•四川)如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,点P在平面ABC内的射影O在AB上. 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=60°,AB=AC=2
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BAC=60°,AB=AC=2