Question

已知F₁，F₂是椭圆的两个焦点，过F₁且与椭圆长轴垂直的直线交椭圆于A，B两点，若△ABF₂是正三角形，则这个椭圆的离心率是________．

Answer 1

分析：根据△ABF₂是正三角形，且直线AB与椭圆长轴垂直，得到F₂F₁是正三角形△ABF₂的高，∠AF₂F₁=30°．在Rt△AF₂F₁中，设|AF₁|=m，可得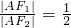，所以|AF₂|=2m，用勾股定理算出|F₁F₂|=m，得到椭圆的长轴2a=|AF₁|+|AF₂|=3m，焦距2c=m，所以椭圆的离心率为e==．
解答：∵△ABF₂是正三角形，
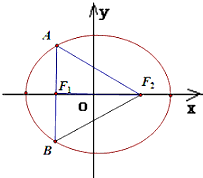
∴∠AF₂B=60°，
∵直线AB与椭圆长轴垂直，
∴F₂F₁是正三角形△ABF₂的高，∠AF₂F₁=×60°=30°，
Rt△AF₂F₁中，设|AF₁|=m，sin30°=，
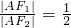∴|AF₂|=2m，|F₁F₂|=
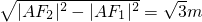
因此，椭圆的长轴2a=|AF₁|+|AF₂|=3m，焦距2c=m
∴椭圆的离心率为e==．
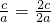故答案为：
点评：本题给出椭圆过焦点垂直于长轴的弦和另一焦点构成直角三角形，求椭圆的离心率．着重考查了椭圆的基本概念和简单几何性质，属于基础题．