题目内容
已知:过点A(0,1)且方向向量为| a |
(1)求实数k的取值范围;
(2)求证:
| AM |
| AN |
分析:(1)只要求出在极限情况,即相切时k的值为多少即可.(2)有切割弦定理可求数量积的值.
解答:解:(1)可设直线l的方程为y=kx+1,与圆的方程:(x-2)2+(y-3)2=1它的圆心(2,3)半径是1.
直线与圆相切时有
=1,解得 k=
或k=
所以,
<k<
.
(2)点A(0,1)在圆外,直线l与⊙C:(x-2)2+(y-3)2=1相交于M、N两点,
•
=|AM||AN|cos0°=|AM||AN|,过A引一切线,切点为T,|有切割弦定理可知:|AM||AN|=|AT|2
是定值.
直线与圆相切时有
| |2k-3+1| | ||
|
4-
| ||
| 3 |
4+
| ||
| 3 |
4-
| ||
| 3 |
4+
| ||
| 3 |
(2)点A(0,1)在圆外,直线l与⊙C:(x-2)2+(y-3)2=1相交于M、N两点,
| AM |
| AN |
是定值.
点评:本题考查圆心到直线的距离,直线方程,在(1)中注意k的范围的问题,容易出错,(2)中的切割弦定理容易疏忽.

练习册系列答案
相关题目
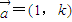 的直线l与⊙C:(x-2)2+(y-3)2=1相交于M、N两点.
的直线l与⊙C:(x-2)2+(y-3)2=1相交于M、N两点. =定值.
=定值.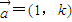 的直线l与⊙C:(x-2)2+(y-3)2=1相交于M、N两点.
的直线l与⊙C:(x-2)2+(y-3)2=1相交于M、N两点.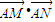 =定值.
=定值.