题目内容
已知椭圆 的右焦点为
的右焦点为 ,离心率为
,离心率为 .
.
(1)若 ,求椭圆的方程; (2)设直线
,求椭圆的方程; (2)设直线 与椭圆相交于
与椭圆相交于 两点,
两点, 分别为线段
分别为线段 的中点.若坐标原点
的中点.若坐标原点 在以
在以 为直径的圆上,且
为直径的圆上,且 ,求
,求 的取值范围.
的取值范围.
【答案】
(1)椭圆方程: (2)
(2) 或
或
【解析】本试题主要是考查了直线与椭圆的位置关系的运用。
(1)因为椭圆 的右焦点为
的右焦点为 ,离心率为
,离心率为 ,那么联立可得a,b的值,得到椭圆方程。
,那么联立可得a,b的值,得到椭圆方程。
(2)设直线 与椭圆方程联立方程组,结合韦达定理和已知中依题意知OM
与椭圆方程联立方程组,结合韦达定理和已知中依题意知OM ON
ON
易知四边形OMF2N为矩形,,所以AF2 B
F2得到参数关系式,然后结合判别式得到范围。
B
F2得到参数关系式,然后结合判别式得到范围。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目




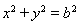

 的右焦点为
的右焦点为 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆 与
与 轴交于
轴交于 两点
两点
 的值;
的值; ,过点
,过点 与圆
与圆 相切的直线
相切的直线 与
与 的另一交点为
的另一交点为 ,求
,求 的面积
的面积
 的右焦点为
的右焦点为 ,
, 点在椭圆上,以
点在椭圆上,以 轴相切,且同时与
轴相切,且同时与 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点 的离心率为 .
的离心率为 . 的右焦点为
的右焦点为 且
且 ,设短轴的一个端点为
,设短轴的一个端点为 ,原点
,原点 到直线
到直线 的距离为
的距离为 ,过原点和
,过原点和 轴不重合的直线与椭圆
轴不重合的直线与椭圆 相交于
相交于 两点,且
两点,且 .
. 的直线
的直线 与椭圆
与椭圆 且使得
且使得 成立?若存在,试求出直线
成立?若存在,试求出直线