题目内容
已知椭圆  的右焦点为
的右焦点为 且
且 ,设短轴的一个端点为
,设短轴的一个端点为 ,原点
,原点 到直线
到直线 的距离为
的距离为 ,过原点和
,过原点和 轴不重合的直线与椭圆
轴不重合的直线与椭圆 相交于
相交于 两点,且
两点,且 .
.
(1) 求椭圆 的方程;
的方程;
(2) 是否存在过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 且使得
且使得 成立?若存在,试求出直线
成立?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】
解析:(1)由 ………………………….1分
………………………….1分
又原点 到直线
到直线 的距离为
的距离为 ,
, ………….2分
………….2分
又 ,
,
故椭圆方程为 ……………………. …………4分
……………………. …………4分
(2)显然当直线 与
与 轴垂直时不可能满足条件……. …………5分
轴垂直时不可能满足条件……. …………5分
故可设存在满足条件的直线 的方程为
的方程为 ,带入椭圆
,带入椭圆 的方程得
的方程得

因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为
 ………………. …………7分
………………. …………7分
因为 ,即
,即
所以 即
即
所以 ,
,
解得 ………………. …………10分
………………. …………10分
因为 为不同的两点,所以
为不同的两点,所以

所以 ………………. …………11分
………………. …………11分
故
所以存在满足条件的直线 ,且其方程为
,且其方程为
【解析】略

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目




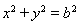

 的右焦点为
的右焦点为 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆 与
与 轴交于
轴交于 两点
两点
 的值;
的值; ,过点
,过点 与圆
与圆 相切的直线
相切的直线 与
与 的另一交点为
的另一交点为 ,求
,求 的面积
的面积
 的右焦点为
的右焦点为 ,
, 点在椭圆上,以
点在椭圆上,以 轴相切,且同时与
轴相切,且同时与 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点 的离心率为 .
的离心率为 .