题目内容
如图,四棱锥P-ABCD中,侧面PAD与底面ABCD互相垂直,且所有棱长均为2,AC∩BD=O.
(Ⅰ)若AB⊥AD,过点O作平面α与平面PBC平行,求所得截面的面积;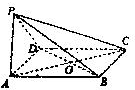
(Ⅱ)若BD=2,二面角A-PC-B的大小为θ,求cosθ的值.
(Ⅰ)若AB⊥AD,过点O作平面α与平面PBC平行,求所得截面的面积;

(Ⅱ)若BD=2,二面角A-PC-B的大小为θ,求cosθ的值.
考点:二面角的平面角及求法,平面与平面平行的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)过O作BN平行线,交AB于E,交DN于F,取AD中点M,连结PM,取PM中点N,连结NE,NF,连结MO,NO,则平面α即平面EFN,由此能求出所得截面的面积.
(Ⅱ)以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,建立空间直角坐标系,分别求出平面APC的法向量和平面PCB的法向量,由此能求出cosθ.
(Ⅱ)以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,建立空间直角坐标系,分别求出平面APC的法向量和平面PCB的法向量,由此能求出cosθ.
解答:
解:(Ⅰ)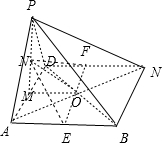 过O作BN平行线,交AB于E,交DN于F,取AD中点M,连结PM,
过O作BN平行线,交AB于E,交DN于F,取AD中点M,连结PM,
取PM中点N,连结NE,NF,连结MO,NO,
则NE∥PB,NF∥PC,
过点O作平面α与平面PBC平行,则平面α即平面EFN,
由已知得EF=2,NE=NF,∴ON⊥EF,
∵NO=
=
,
∴所得截面的面积S=
×EF×NO=
×2×
=
.
(Ⅱ)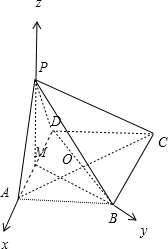 以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,
以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,
建立空间直角坐标系,
A(1,0,0),P(0,0,
),C(-2,
,0),B(0,
,0),
=(1,0,-
),
=(0,
,-
),
=(-2,
,-
),
设平面APC的法向量
=(x,y,z),
则
,取z=
,得
=(3,3
,
),
设平面PCB的法向量
=(a,b,c),
则
,取b=1,得
=(0,1,1),
cosθ=|cos<
,
>|=
=
=
.
 过O作BN平行线,交AB于E,交DN于F,取AD中点M,连结PM,
过O作BN平行线,交AB于E,交DN于F,取AD中点M,连结PM,取PM中点N,连结NE,NF,连结MO,NO,
则NE∥PB,NF∥PC,
过点O作平面α与平面PBC平行,则平面α即平面EFN,
由已知得EF=2,NE=NF,∴ON⊥EF,
∵NO=
| MN2+MO2 |
| ||
| 2 |
∴所得截面的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)
 以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,
以AD中点M为原点,MA为x轴,MB为y轴,MP为z轴,建立空间直角坐标系,
A(1,0,0),P(0,0,
| 3 |
| 3 |
| 3 |
| PA |
| 3 |
| PB |
| 3 |
| 3 |
| PC |
| 3 |
| 3 |
设平面APC的法向量
| n |
则
|
| 3 |
| n |
| 3 |
| 3 |
设平面PCB的法向量
| m |
则
|
| m |
cosθ=|cos<
| n |
| m |
|
| ||||
|
|
4
| ||||
|
2
| ||
| 13 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,线线角、线面角、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
相关题目
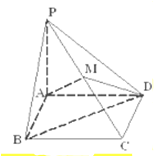 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,点M是棱PC的中点,AM⊥平面PBD
(1)求四棱锥P-ABCD的体积;
(2)求平面PAD与平面AMD所成二面角的大小.
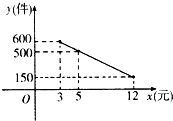 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.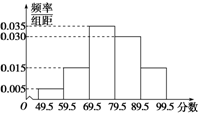 某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )
某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )