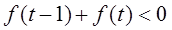题目内容
(本题满分12分)解下列关于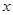 的不等式:
的不等式: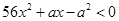
①当 时,
时, ,∴原不等式的解集为
,∴原不等式的解集为 ;
;
②当 ∴原不等式的解集为:
∴原不等式的解集为:
③当 ,∴原不等式解集为
,∴原不等式解集为
解析试题分析:对于一元二次不等式的求解,先确定方程的根,然后结合图像与性质来得到不等式的解集。
解:方程 的根为
的根为 ∵
∵ 于是
于是
①当 时,
时, ,∴原不等式的解集为
,∴原不等式的解集为 ;
;
②当 ∴原不等式的解集为:
∴原不等式的解集为:
③当 ,∴原不等式解集为
,∴原不等式解集为
考点:本题主要考查了一元二次不等式的解集的求解的运用。
点评:解决该试题的关键是对于二次函数的开口方向和根的大小来运用分类讨论的思想来得到不等式的解集问题的运用。

练习册系列答案
相关题目
 ﹞的最大值并求出相应的x值.
﹞的最大值并求出相应的x值.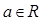 ,函数
,函数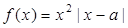 .
.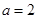 时,求使
时,求使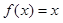 成立的
成立的 的集合;
的集合;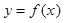 在区间
在区间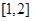 上的最小值.
上的最小值. 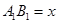 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于 的函数
的函数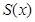 的解析式;
的解析式;
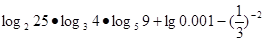
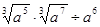
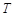 是时间
是时间 的函数:
的函数: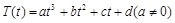 ,其中温度的单位是
,其中温度的单位是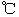 ,时间单位是小时,
,时间单位是小时,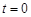 表示12:00,
表示12:00,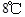 ,12:00的温度为
,12:00的温度为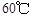 ,13:00的温度为
,13:00的温度为 ,且已知该物体的温度在8:00和16:00有相同的变化率.
,且已知该物体的温度在8:00和16:00有相同的变化率.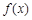 在区间
在区间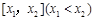 上的平均值为
上的平均值为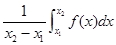 ,求该物体在8:00到16:00这段时间内的平均温度.
,求该物体在8:00到16:00这段时间内的平均温度.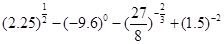 ;
;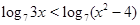 .
.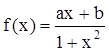 是定义在
是定义在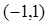 上的奇函数,且
上的奇函数,且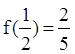
 的解析式。
的解析式。 在
在 上是增函数。
上是增函数。